23 Model temelleri
23.1 Giriş
Bir modelin amacı, bir veri setinin düşük boyutlu basit bir özetini sunmaktır. Bu kitap kapsamında, verileri örüntülere ve örüntü dışında kalan kalıntılara (residuals) ayırmak için modelleri kullanacağız. Güçlü örüntüler daha hassas eğilimleri (trend) gizlerler, bu nedenle bir veri setini anlamaya çalışırken yapıyı katmanlara ayırmak için modeller kullanırız.
Bununla birlikte, gerçek, ilginç veri setleri üzerinde modelleri kullanmaya başlamadan önce, modellerin çalışma temellerini anlamanız gerekir. Bu nedenle, kitabın bu bölümü eşsizdir çünkü yalnızca simüle edilmiş veri setleri kullanılmıştır. Bu veri setleri oldukça basit, hatta hiç ilginç olmayan, ancak aynı teknikleri bir sonraki bölümde gerçek verilere uygulamadan önce modellemenin özünü anlamanıza yardımcı olacaklar.
Bir model iki kısımdan oluşur:
İlk önce, elde etmek istediğiniz kalıbı kesin ve genelleyici şekilde ifade eden bir modeller ailesi tanımlanır. Örneğin, örüntü düz bir çizgi veya kuadrat bir eğri olabilir. Model ailesi
y = a_1 * x + a_2veyay = a_1 * x ^ a_2gibi bir denklem olarak ifade edilir. Burada, x ve y verilerinizden bilinen değişkenlerdir ve a_1 ile a_2, farklı örüntüleri yakalamak için değişken olabilecek parametrelerdir.Sonra, verilerinize ailedeki en yakın modeli bularak uygun bir model üretilir. Bu, genelleyici model ailesini alır ve onu
y = 3 * x + 7veyay = 9 * x ^ 2gibi belirli bir hale getirir.
Uygulanan bir modelin, modeller ailesinden seçilmiş en yakın model olduğunu anlamak önemlidir. Bu, “en iyi” modele sahip olduğunuz anlamına gelir (bazı kriterlere göre); iyi bir modele sahip olduğunuz ve kesinlikle modelin “gerçek” olduğu anlamına gelmez. George Box, bu meşhur aforizmasıyla bunu oldukça iyi anlatır:
Bütün modeller yanlıştır, ancak bazıları kullanışlıdır.
Alıntının tam metni de okumaya değerdir:
Şu an gerçek dünyada var olan herhangi bir sistemin, basit bir modelle tam olarak sunulabilmesi oldukça dikkat çekici olurdu. Gerçi zekice seçilmiş parsimoni modelleri genel olarak oldukça faydalı yaklaşımlar sağlamaktadır. Örneğin bir R sabiti üzerinden “ideal” bir gaz basıncının T sıcaklık, V hacim ve P basınca bağlı olarak üretilmiş PV = RT kanunu, her hangi bir gaz için tam doğru değildir, ancak sıklıkla yararlı bir yaklaşım sunar ve dahası gaz molekülleri fiziksel davranışlarının görünümünden meydana geldiği için yapısı bilgilendiricidir.
Böyle bir model için “model gerçek midir?” sorusunu sormaya gerek yoktur. Eğer “gerçek”, “tamamen gerçek” olmak manasında ise, cevap “Hayır” olmalıdır. İlgilenilen tek soru “model aydınlatıcı ve kullanışlı mı?” olmalıdır.
Bir modelin amacı gerçeği ortaya çıkarmak değil, yine de kullanışlı olan basit bir yaklaşımı keşfetmektir.
23.2 Basit bir model
modelr paketinde yer alan “sim1” simüle veri setine bakalım. x vey olmak üzere iki sürekli değişken içerir. Aralarında nasıl bir ilişki olduğunu görmek için onları çizdirelim:
ggplot(sim1, aes(x, y)) +
geom_point()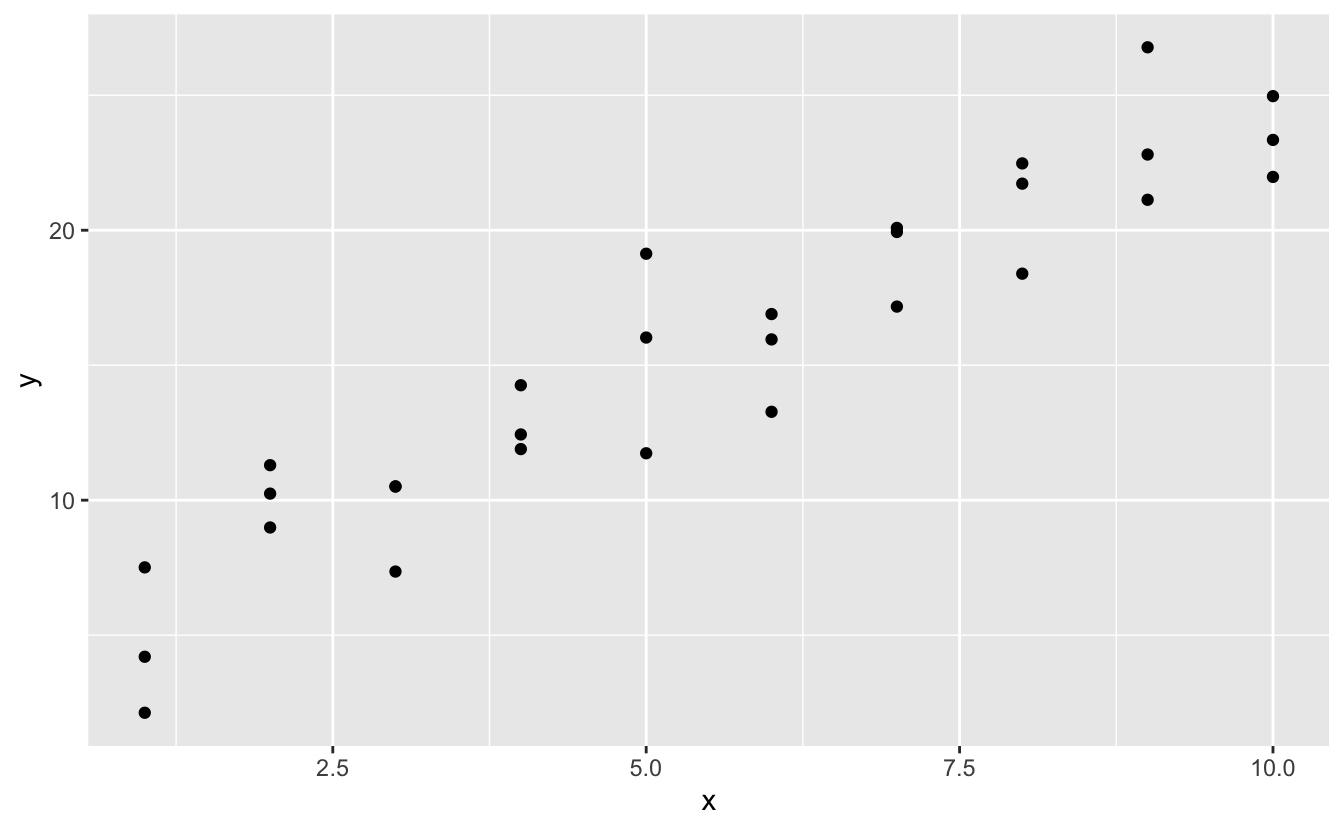
Verilerdeki güçlü örüntüyü görebilirsiniz. Bu örüntüyü yakalamak ve açık hale getirmek için bir model kullanalım. Modelin temel formunu sağlamak bizim işimiz. Bu örnekte ilişki doğrusal gözükmektedir, örneğin y = a_0 + a_1 * x. Bu aileden hangi modellerin bir kaçını rastgele üretip ve onları verilerin üzerine yerleştirdiğimizde nasıl göründüklerini hissederek başlayalım. Bu basit örnekte, bir eğim alarak parametrelerle kesiştiren geom_abline()’ı kullanabilirsiniz. Daha sonra herhangi bir modelle çalışan daha genel teknikleri öğreneceğiz.
models <- tibble(
a1 = runif(250, -20, 40),
a2 = runif(250, -5, 5)
)
ggplot(sim1, aes(x, y)) +
geom_abline(aes(intercept = a1, slope = a2), data = models, alpha = 1/4) +
geom_point() 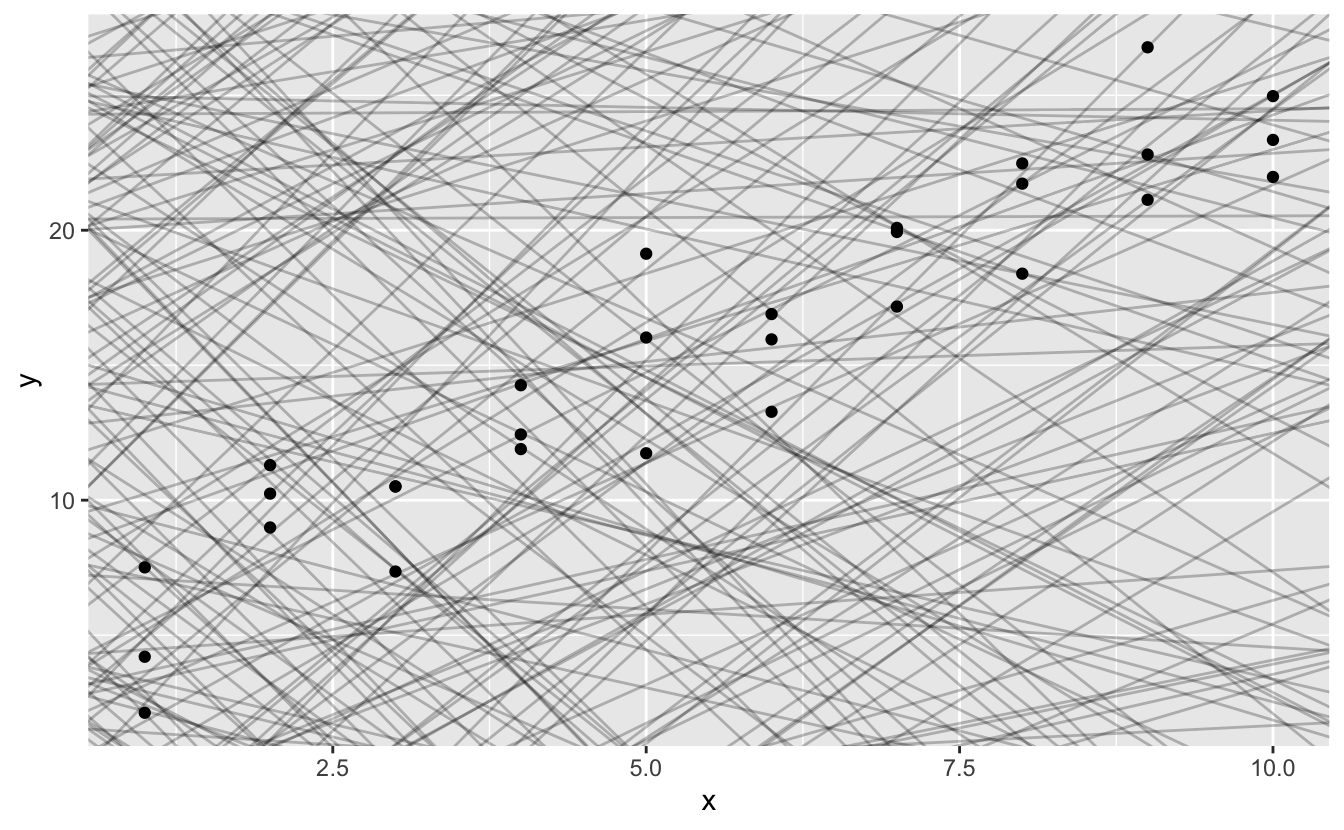
Bu grafik üzerinde 250 model bulunuyor, ama birçoğu gerçekten kötü görünüyor! “İyi bir model verilere ‘yakın’ olandır” görüşümüzü destekler nitelikte iyi bir model bulmalıyız. Veri ile model arasındaki mesafeyi ölçecek bir yola ihtiyacımız var. Sonrasında bu verilerden en küçük mesafeyle modeli oluşturan a_0 ve a_1 değerlerini bulup modele uyarlayabiliriz.
Aşağıdaki diyagramdaki gibi her nokta ve model arasındaki dikey mesafeyi bulmak kolay bir başlangıç olacaktır. (Tek tek mesafeleri görebilmeniz için x değerlerini biraz kaydırdığımı unutmayın.)
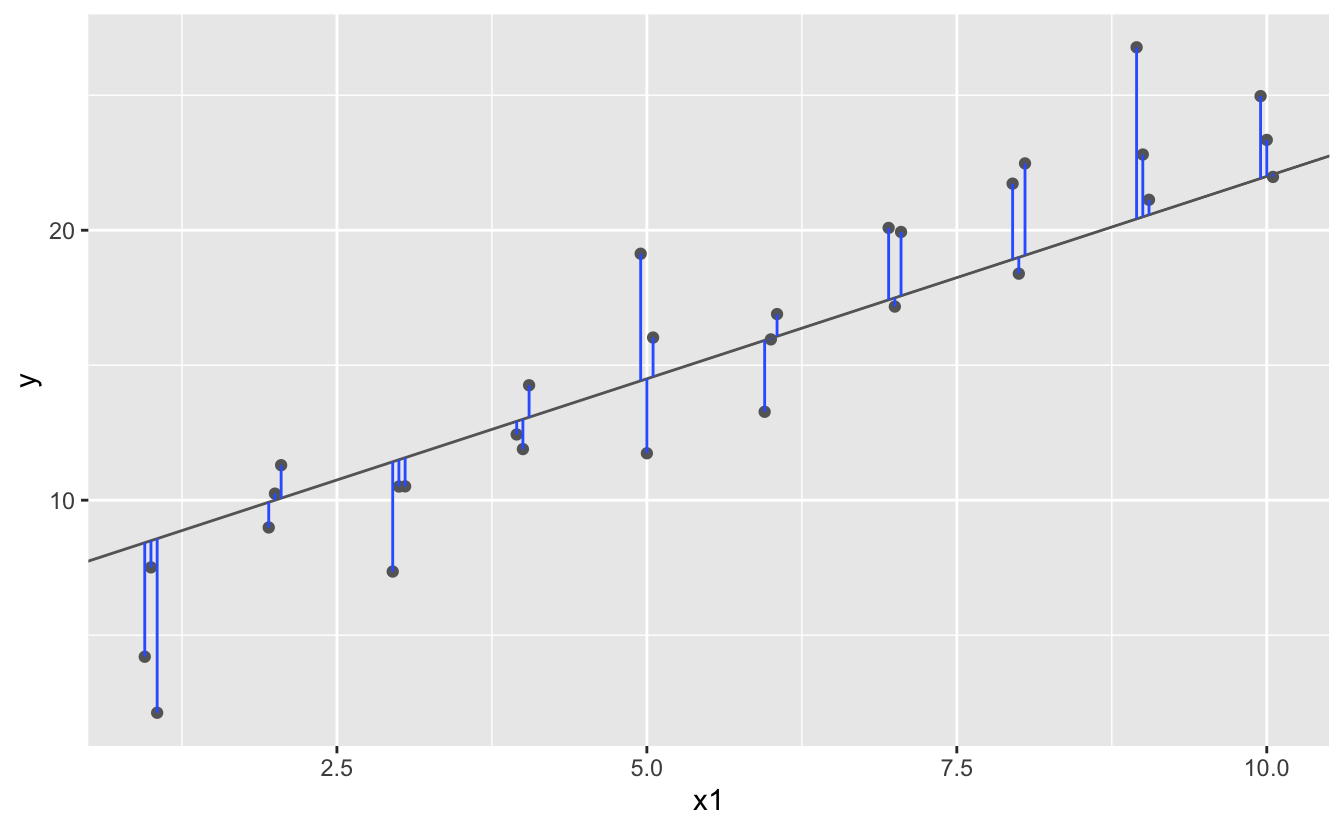
Bu mesafe, sadece model tarafından verilen y değeri ( tahmin) ile verideki gerçek y değeri ( yanıt) arasındaki farktır.
Bu mesafeyi hesaplamak için önce model ailemizi R fonksiyonuna dönüştürüyoruz. Bu, model parametrelerini ve verileri girdi olarak alır ve model tarafından çıktı olarak öngörülen değerleri verir:
model1 <- function(a, data) {
a[1] + data$x * a[2]
}
model1(c(7, 1.5), sim1)
#> [1] 8.5 8.5 8.5 10.0 10.0 10.0 11.5 11.5 11.5 13.0 13.0 13.0 14.5 14.5 14.5
#> [16] 16.0 16.0 16.0 17.5 17.5 17.5 19.0 19.0 19.0 20.5 20.5 20.5 22.0 22.0 22.0Sonrasında, öngörülen ve gerçek değerler arasındaki toplam mesafeyi hesaplayacak bir yola ihtiyacımız var. Başka bir deyişle, yukarıdaki grafik 30 farklı mesafeyi göstermektedir: Bunu tek bir sayıya nasıl indirebiliriz?
İstatistikte bunu yapmanın yaygın bir yolu “kök-ortalama-kare sapma” kullanmaktır. Bu mesafe, burada değinmeyeceğimiz birçok çekici matematiksel özelliğe sahiptir. Şimdilik sadece benim sözüme güvenin!
measure_distance <- function(mod, data) {
diff <- data$y - model1(mod, data)
sqrt(mean(diff ^ 2))
}
measure_distance(c(7, 1.5), sim1)
#> [1] 2.67Şimdi yukarıda tanımlanan tüm modellerin mesafesini hesaplamak için purrr’ı kullanabiliriz. Mesafe fonksiyonumuz, uzunluğu iki olan sayısal vektör şeklinde bir model beklediğinden, yardımcı bir fonksiyona ihtiyacımız var.
sim1_dist <- function(a1, a2) {
measure_distance(c(a1, a2), sim1)
}
models <- models %>%
mutate(dist = purrr::map2_dbl(a1, a2, sim1_dist))
models
#> # A tibble: 250 × 3
#> a1 a2 dist
#> <dbl> <dbl> <dbl>
#> 1 -15.2 0.0889 30.8
#> 2 30.1 -0.827 13.2
#> 3 16.0 2.27 13.2
#> 4 -10.6 1.38 18.7
#> 5 -19.6 -1.04 41.8
#> 6 7.98 4.59 19.3
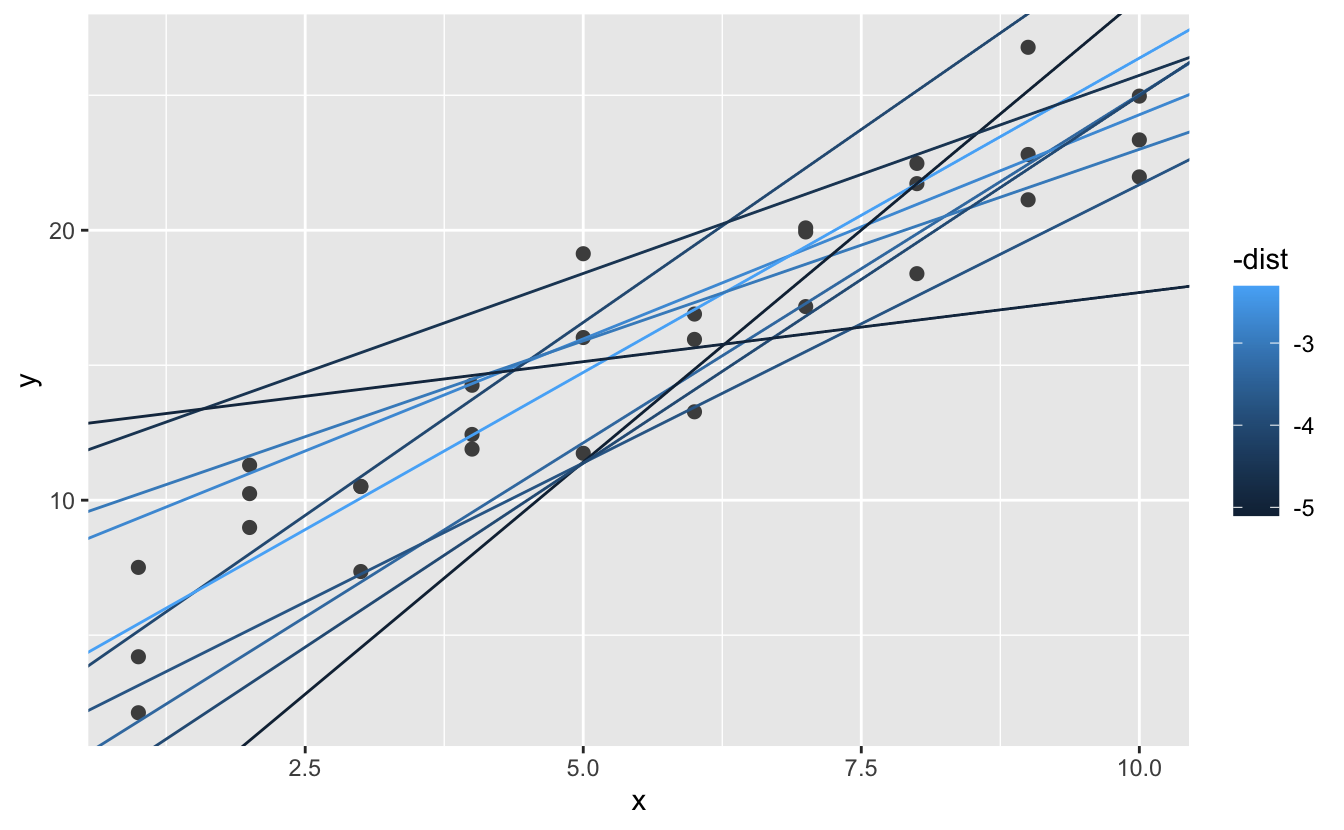
#> # … with 244 more rowsArdından, veriler üzerine en iyi 10 modeli yerleştirelim. Modelleri -dist kullanarak renklendirdim: en iyi modellerin (örn; en kısa mesafede olanların) en parlak renkler ile göstermenin kolay bir yoludur.
ggplot(sim1, aes(x, y)) +
geom_point(size = 2, colour = "grey30") +
geom_abline(
aes(intercept = a1, slope = a2, colour = -dist),
data = filter(models, rank(dist) <= 10)
)
Ayrıca bu modelleri gözlemler olarak düşünebilir ve a1 ile a2 arasındaki dağılım grafiğini tekrar -dist ile renklendirerek görselleştirebiliriz. Artık modelin verilerle karşılaştırmasını doğrudan göremiyoruz, ancak birçok modeli tek seferde görebiliyoruz. Yine, bu kez altlarına kırmızı daireler çizerek en iyi 10 modeli vurguladım.
ggplot(models, aes(a1, a2)) +
geom_point(data = filter(models, rank(dist) <= 10), size = 4, colour = "red") +
geom_point(aes(colour = -dist))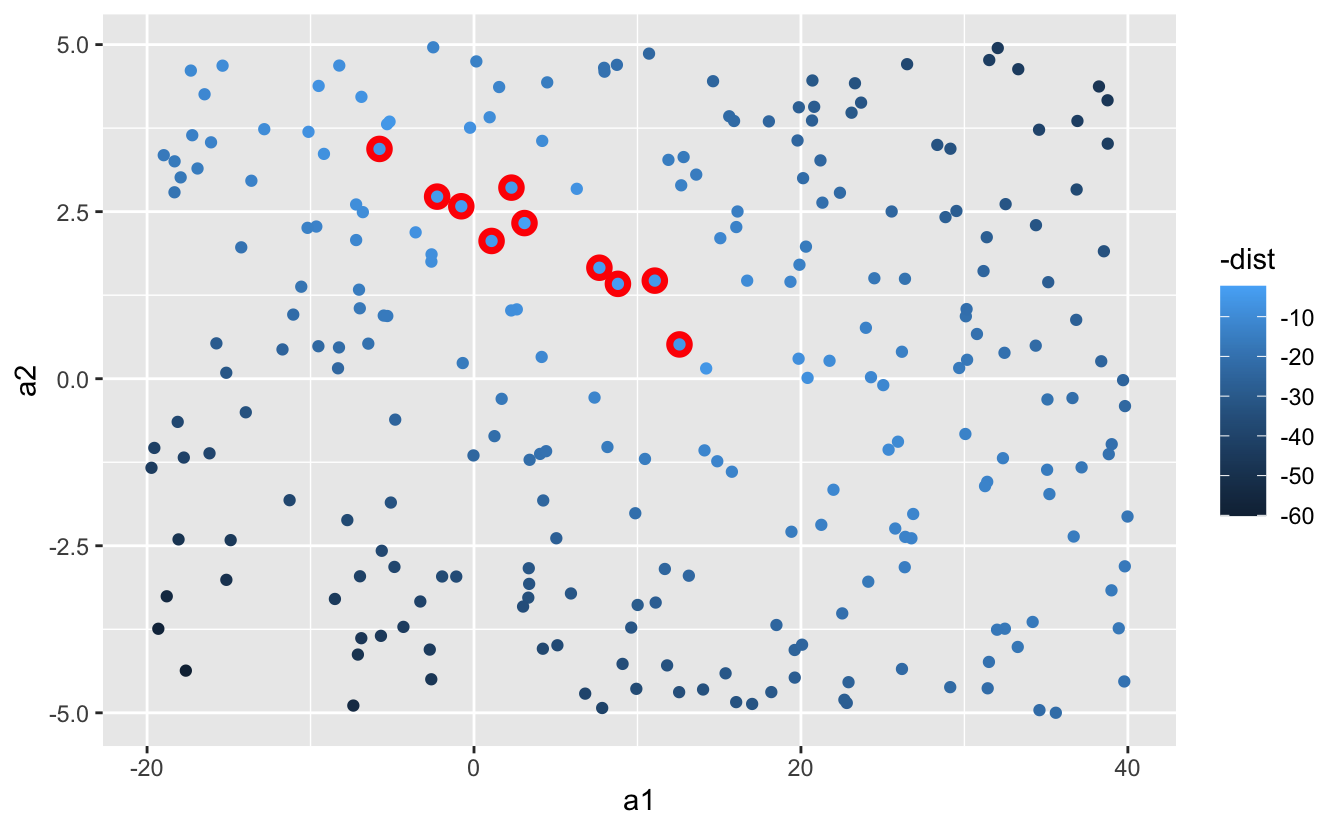
Pek çok rastgele model denemek yerine, daha sistematik olabilir ve eşit aralıklarla yerleştirilmiş bir nokta ızgarası oluşturabiliriz (buna ızgara arama yöntemi denmektedir). Yukarıdaki grafikte en iyi modellerin olduğu yere bakarak ızgaraya ait parametreleri kabaca ele aldım.
grid <- expand.grid(
a1 = seq(-5, 20, length = 25),
a2 = seq(1, 3, length = 25)
) %>%
mutate(dist = purrr::map2_dbl(a1, a2, sim1_dist))
grid %>%
ggplot(aes(a1, a2)) +
geom_point(data = filter(grid, rank(dist) <= 10), size = 4, colour = "red") +
geom_point(aes(colour = -dist)) 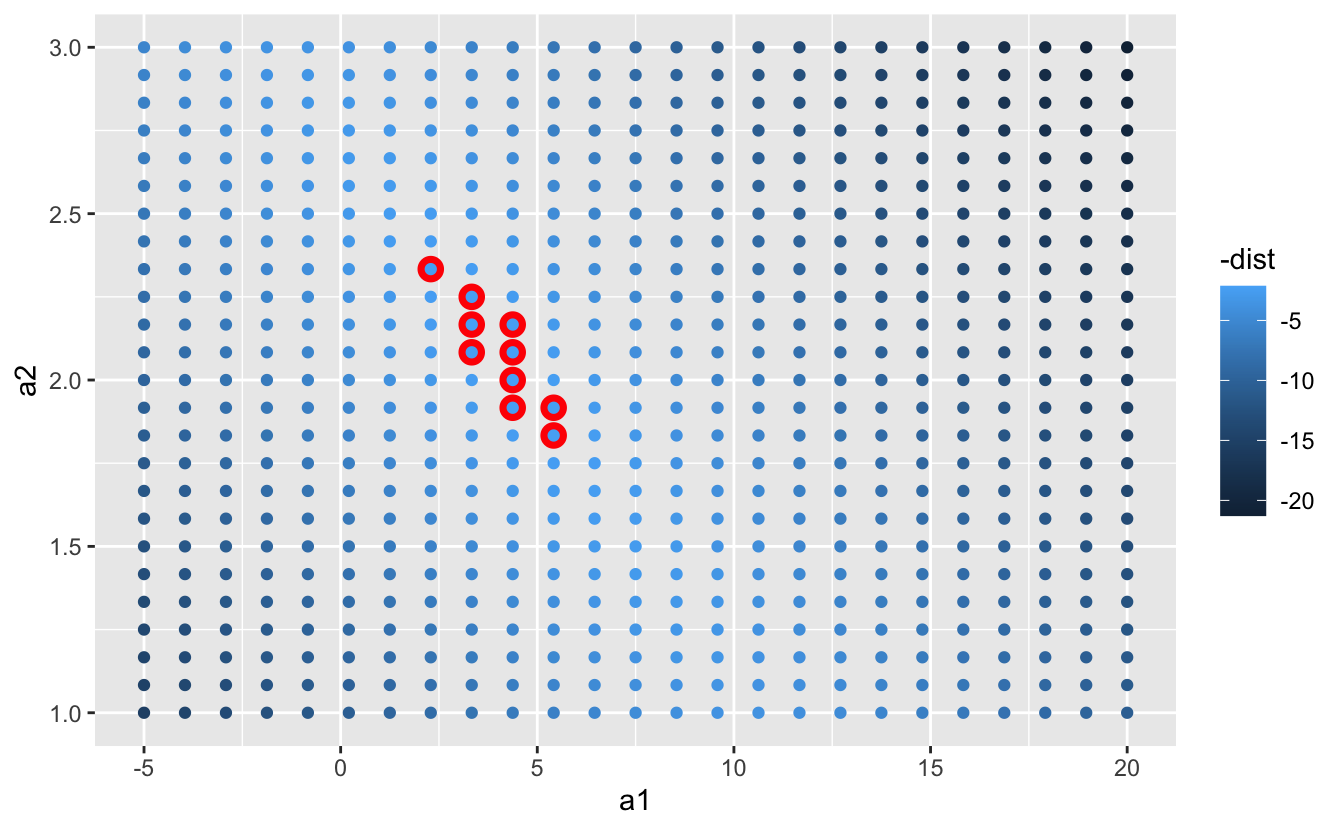
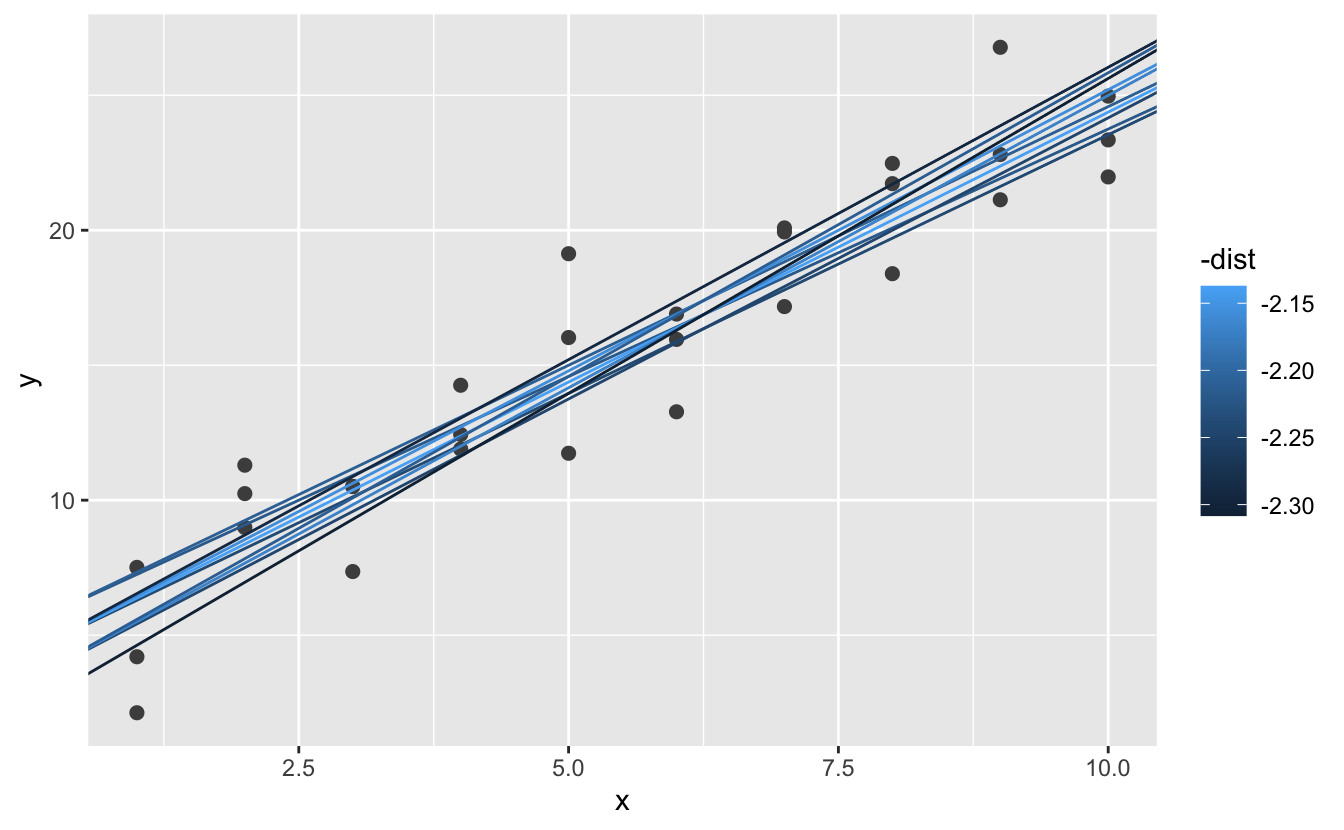
En iyi 10 modeli orijinal veriler üzerine yerleştirdiğinizde, hepsi oldukça iyi görünüyor:
ggplot(sim1, aes(x, y)) +
geom_point(size = 2, colour = "grey30") +
geom_abline(
aes(intercept = a1, slope = a2, colour = -dist),
data = filter(grid, rank(dist) <= 10)
)
Izagarayı giderek daha ince hale getirerek en iyi modelin üzerine denk gelecek şekilde daraltmayı düşünebilirsiniz. Ancak bu problemi çözmenin daha iyi bir yolu var: Newton-Raphson araştırması denilen sayısal bir küçültme aracı. Newton-Raphson’un yaklaşımı oldukça basittir: bir başlangıç noktası seçip en dik eğim için çevresine bakmalısınız. Daha sonra o eğimden biraz aşağı doğru kayın ve bunu daha fazla aşağıya inemeyeceğiniz seviyeye gelene kadar tekrar edin. R’da bunu optim() ile yapabiliriz:
best <- optim(c(0, 0), measure_distance, data = sim1)
best$par
#> [1] 4.22 2.05
ggplot(sim1, aes(x, y)) +
geom_point(size = 2, colour = "grey30") +
geom_abline(intercept = best$par[1], slope = best$par[2])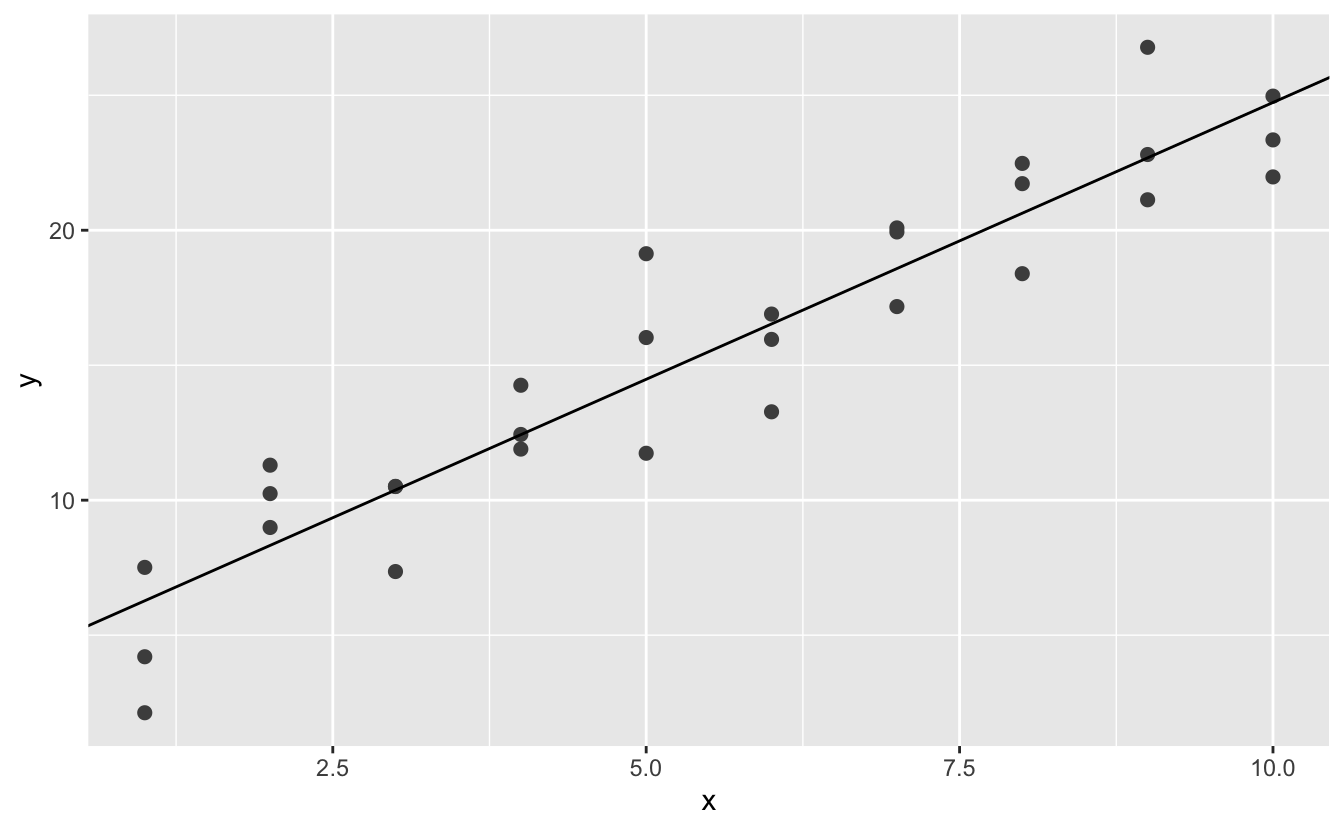
optim()’in nasıl çalıştığıyla ilgili detaylara fazla takılmayın. Burada önemli olan yaklaşımdır. Bir model ile veri seti arasındaki mesafeyi tanımlayan bir işleve sahipseniz, modelin parametrelerini değiştirerek bu mesafeyi en aza indirebilen bir algoritma varsa, en iyi modeli bulabilirsiniz demektir. Bu yaklaşım ile ilgili en güzel şey, bir denklem için yazabileceğiniz herhangi bir model ailesi için uygulanabilir olmasıdır.
Çok daha geniş bir ailenin özel bir durumundan dolayı bu model için kullanabileceğiniz bir yaklaşım daha var: doğrusal modelleme. Doğrusal bir model genel olarak y = a_1 + a_2 * x_1 + a_3 * x_2 + ... + a_n * x_(n - 1) şeklinde ifade edilebilir. Dolayısıyla bu basit model, n’nin 2 ve x_1’in x olduğu genel doğrusal modele eşdeğerdir. R’da özellikle lm() adı verilen doğrusal modellerin uyarlanması için özel olarak dizayn edilmiş bir araç mavcuttur. lm() model ailesini belirtmenin özel bir yöntemine sahiptir: formüller. Formüller y ~ x gibi görünür; lm (), y = a_1 + a_2 * x gibi bir fonksiyona dönüştürülmektedir. Modele uygulayabilir ve çıktısına bakabiliriz:
sim1_mod <- lm(y ~ x, data = sim1)
coef(sim1_mod)
#> (Intercept) x
#> 4.22 2.05Bunlar optim() ile aldığımız değerlerin aynısıdır! Arka planda lm(), optim()’i kullanmaz, ancak doğrusal modellerin matematiksel yapısından faydalanır. lm() karmaşık bir algoritma ile geometri, matematik ve doğrusal cebir arasındaki bazı ilişkileri kullanarak en karmaşık modeli tek bir adımda bulabilmektedir. Bu yaklaşım hem daha hızlıdır hem de kesinlikle tasarruf sağlar.
23.2.1 Alıştırmalar
Doğrusal modelin bir dezavantajı, alışılmadık değerlere duyarlı olmasıdır, çünkü mesafe karesi şeklinde ifade edilmektedir. Aşağıda simüle edilmiş verilere doğrusal bir model uyarlayarak sonuçları görselleştiriniz. Farklı simüle veri kümeleri oluşturmak için modeli birkaç kez yeniden çalıştırın. Model hakkında dikkatinizi ne çekmektedir?
sim1a <- tibble( x = rep(1:10, each = 3), y = x * 1.5 + 6 + rt(length(x), df = 2) )Doğrusal modelleri daha tutarlu hale getirmenin bir yolu, farklı bir mesafe ölçümü kullanmaktır. Örneğin, kök-ortalama-kare mesafe yerine, ortalama-mutlak mesafeyi kullanabilirsiniz:
measure_distance <- function(mod, data) { diff <- data$y - model1(mod, data) mean(abs(diff)) }Bu modeli yukarıdaki verilere uydurmak için
optim ()yöntemini kullanın ve doğrusal modelle karşılaştırın.Sayısal optimizasyon gerçekleştirme konusundaki zorluklardan biri, yalnızca bir lokal optimum bulmanın garanti olmasıdır. Bunun gibi üç parametreli bir modeli optimize etmedeki problem nedir?
model1 <- function(a, data) { a[1] + data$x * a[2] + a[3] }
23.3 Modellerin görselleştirilmesi
Yukarıdaki gibi basit modeller için, model ailesini ve kullanılan katsayıları dikkatlice inceleyerek modelin hangi kalıba uyguğunu kavrayabilirsiniz. Eğer sadece modelleme üzerine bir istatistik dersi almak isterseniz, çok fazla zaman harcamanız gerekecektir. Ne var ki, burada farklı bir yol izleyeceğiz. Tahminlerine bakarak bir modeli anlamaya odaklanacağız. Bu durum bize büyük bir avantaj sunmaktadır: Tahmine dayalı her türlü model, tahminde bulunur (aksi halde neden kullanılsınlar?). Bu sebeple, her tür tahmine dayalı bir modeli anlamak için aynı teknikleri kullanabiliriz.
Tahmin değerlerini veriden çıkardıktan sonra geriye kalan ki onlara “artık” (residual) diyoruz, modelin neyi yakalamadığını görmek açısından faydalı olacaktır. Artıklar güçlü araçlardır çünkü dikkat çekici örüntüleri ortadan kaldırarak modelleri kullanmamızı ve böylece daha hassas eğilimler yakalamamızı sağlar.
23.3.1 Tahminler
Bir modele ait tahminleri görselleştirmek için, verilerimizin bulunduğu bölgeyi kapsayan eşit aralıklı bir değerler ızgarası oluşturarak işe başlamalıyız. Bunu yapmanın en kolay yolu modelr :: data_grid () kullanmaktır. İlk argüman bir veri tablosudur, sonraki her argüman için benzersiz değişkenleri bulur ve ardından tüm kombinasyonları oluşturur:
grid <- sim1 %>%
data_grid(x)
grid
#> # A tibble: 10 × 1
#> x
#> <int>
#> 1 1
#> 2 2
#> 3 3
#> 4 4
#> 5 5
#> 6 6
#> # … with 4 more rows(Modelimize daha fazla değişken eklemeye başladığımızda bu daha ilginç hale gelecektir.)
Ardından tahminde kullanılan değişkenleri ekleyelim. Veri tablosu ve modeli elde etmeye yarayan modelr::add_predictions()’ı kullanacağız. Modelden elde edilen tahminleri veri tablosu içerisinde yeni bir sütuna ekleyeceğiz:
grid <- grid %>%
add_predictions(sim1_mod)
grid
#> # A tibble: 10 × 2
#> x pred
#> <int> <dbl>
#> 1 1 6.27
#> 2 2 8.32
#> 3 3 10.4
#> 4 4 12.4
#> 5 5 14.5
#> 6 6 16.5
#> # … with 4 more rows(Bu fonksiyonu, orjinal veri kümenize tahminleri eklemek için de kullanabilirsiniz.)
Devamında, tahminleri çizdiriyoruz. Tüm bu ekstra işleri sadece geom_abline() kullanmak varken neden yaptığımızı merak edebilirsiniz. Ancak bu yaklaşımın avantajı, en basitinden en karmaşığına kadar R’deki herhangi bir modelle çalışacak olmasıdır. Yalnızca görselleştirme becerilerinizle sınırlısınız. Daha karmaşık model türlerinin nasıl görselleştirileceği hakkında daha fazla fikir için http://vita.had.co.nz/papers/model-vis.html adresini ziyaret edebilirsiniz.
ggplot(sim1, aes(x)) +
geom_point(aes(y = y)) +
geom_line(aes(y = pred), data = grid, colour = "red", size = 1)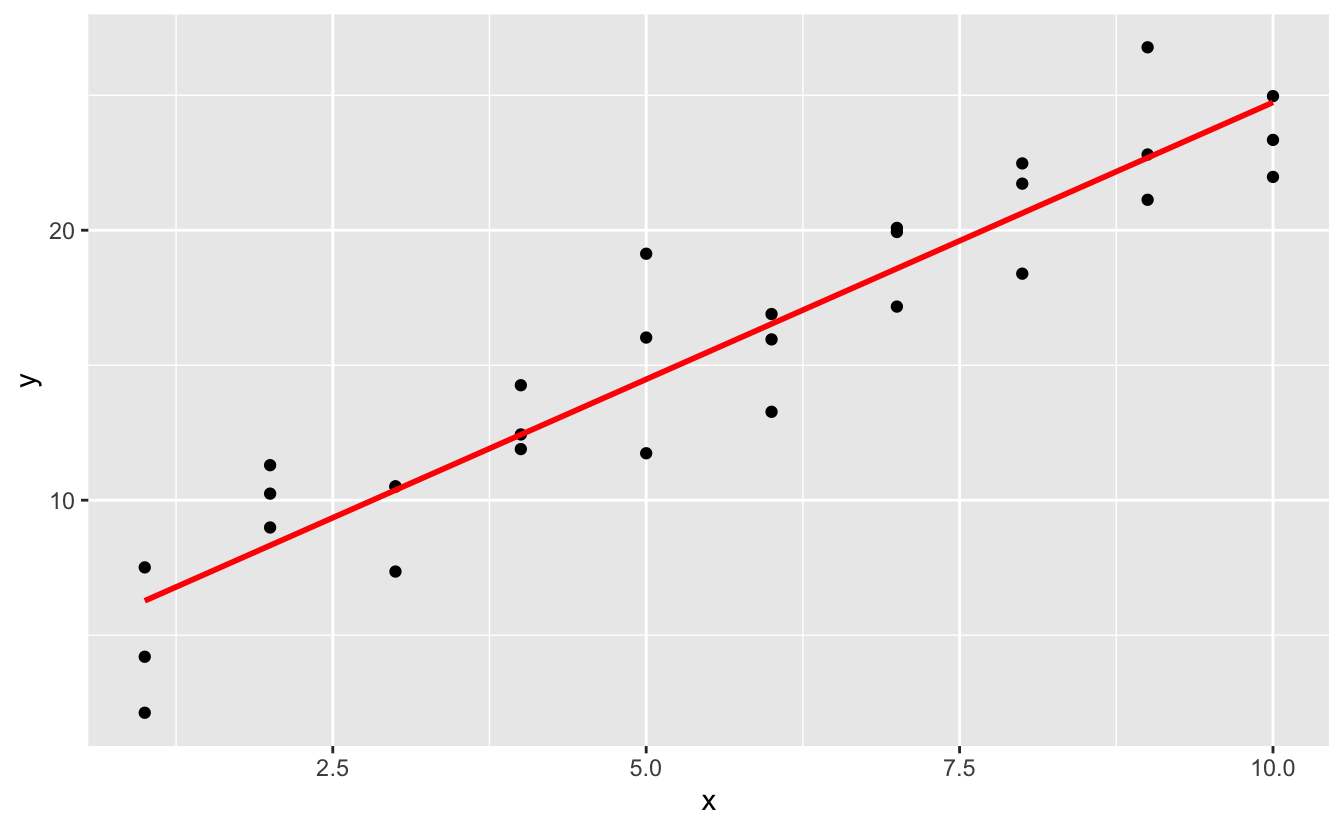
23.3.2 Artıklar
Tahminlerin diğer yüzü artıklarıdr. Tahminler, modelin elde ettiği kalıbı bize söylerken, artıklar de modelin neyi kaçırdığını bize söylerler. Artıklar sadece yukarıda hesapladığımız gözlemlenen ve öngörülen değerler arasındaki mesafelerdir.
Aynı add_predictions()’da olduğu gibi, add_residuals() ile veriye artıklar eklenebilir. Ancak ne var ki orjinal veri setini kullandığımızı ve onun üretilmiş bir ızgara sistemi olmadığını unutmamalısınız. Bunun nedeni, artıkları hesaplamak için gerçek y değerlerine ihtiyacımız vardır.
sim1 <- sim1 %>%
add_residuals(sim1_mod)
sim1
#> # A tibble: 30 × 3
#> x y resid
#> <int> <dbl> <dbl>
#> 1 1 4.20 -2.07
#> 2 1 7.51 1.24
#> 3 1 2.13 -4.15
#> 4 2 8.99 0.665
#> 5 2 10.2 1.92
#> 6 2 11.3 2.97
#> # … with 24 more rowsArtıkların model hakkında bize neler söylediğini anlamanın birkaç farklı yolu vardır. Bunlardan bir tanesi, artıkların yayılımını anlamamıza yardımcı olacak bir frekans poligonu çizmektir:
ggplot(sim1, aes(resid)) +
geom_freqpoly(binwidth = 0.5)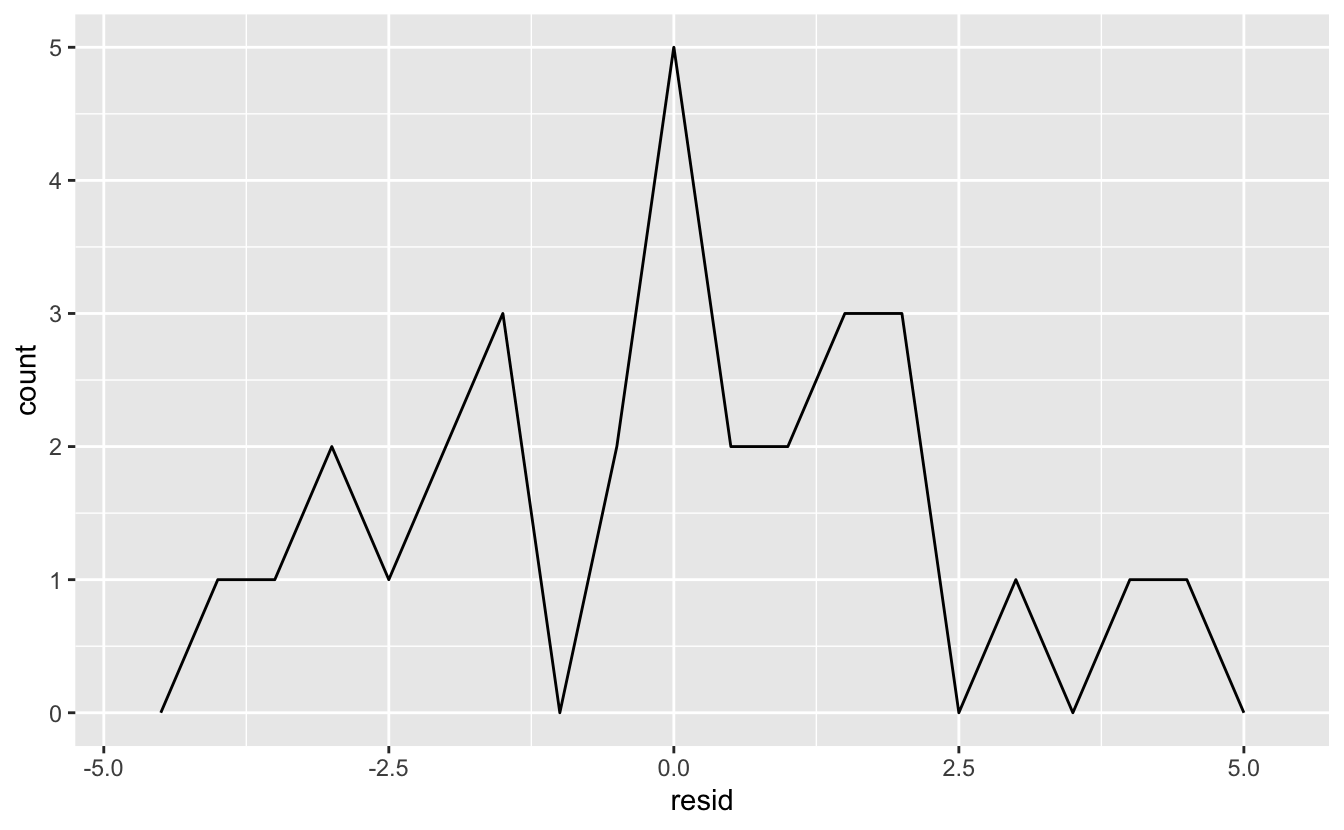
Bu, modelin kalitesini kalibre etmenize yardımcı olur: tahminler, gözlemlenen değerlerden ne kadar uzakta? Artıkların ortalamasının daima 0 olacağını unutmayın.
Çoğunlukla, orjinal tahminler yerine artıkları kullanarak grafikleri oluşturmak isteyeceksiniz. Bir sonraki bölümde bundan fazlaca göreceksiniz.
ggplot(sim1, aes(x, resid)) +
geom_ref_line(h = 0) +
geom_point() 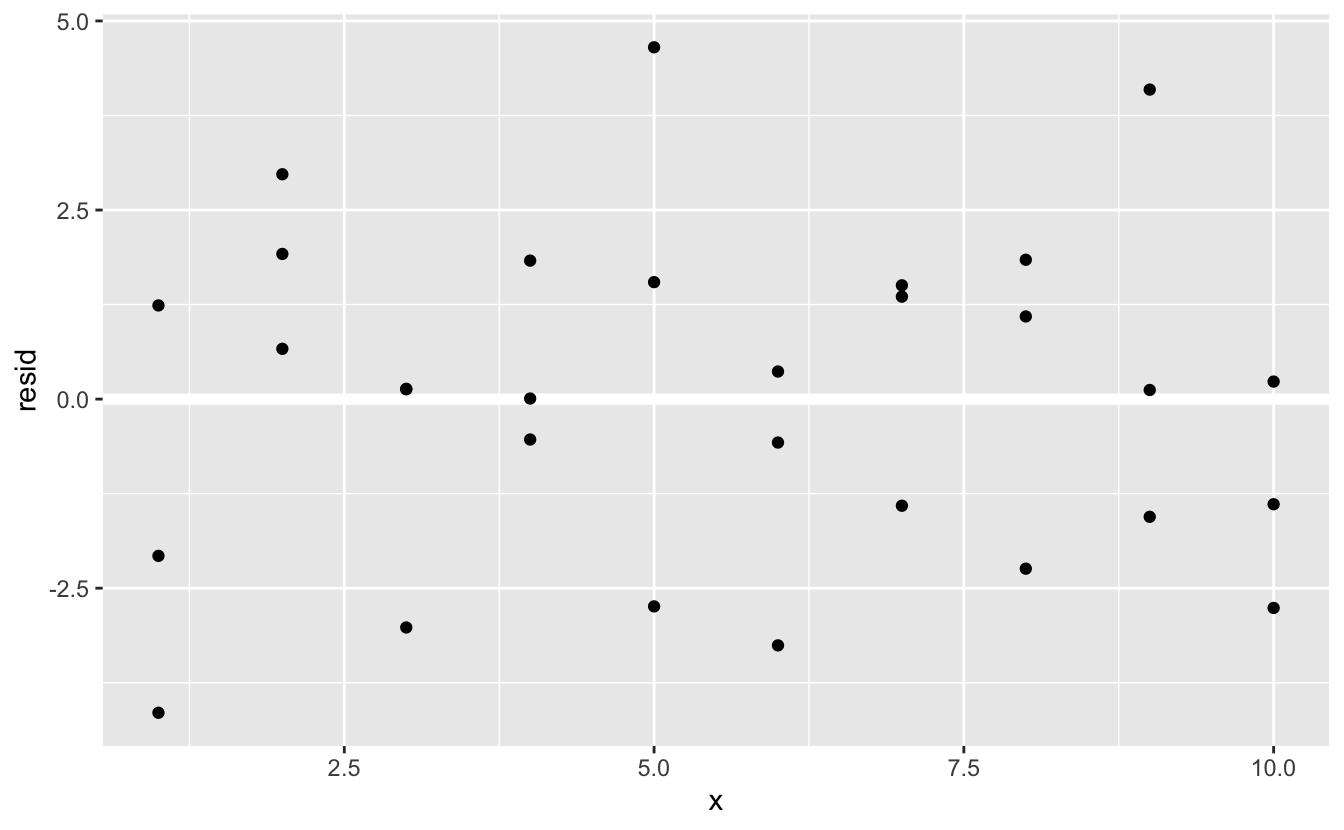
Bu rastgele parazitliğe benziyor, sanırım modelimiz veri setindeki örüntüleri elde etmek için iyi bir iş çıkardı.
23.3.3 Uygulamalar
Düz bir hat uygulamak için
lm()kullanmak yerine, daha az pürüzlü bir eğri içinloess()de kullanabilirsiniz. Model uygulama, ızgara oluşturma, tahminler vesim1’in görselleştirilmesi içinlm()yerineloess()kullanarak işlemi tekrarlayınız.geom_smooth()’a kıyasla sonuçlar nasıldır?add_predictions(),gather_predictions()vespread_predictions()ile eşleştirilmiştir. Bu üç fonksiyon birbirinden nasıl farklılık gösterir?Geom_ref_line ()’nın görevi nedir? Hangi paket içerisinde yer alır? Niçin artıkları gösteren grafiklerde referans çizgisini göstermek faydalı ve önemlidir?
4 . Neden mutlak artık frekans poligonlarına bakmak isteyebilirsiniz? İşlenmemiş rezidüeller üzerinde çalışmanın artıları ve eksileri nelerdir?
23.4 Formüller ve model aileleri
Daha önce facet_wrap() ve facet_grid() kullanırken formülleri gördünüz. R’da, formüller “özel davranış” sergileme imkanı sunarlar. Doğrudan değişkenleri değerlendirmek yerine onları, fonksiyon tarafından yorumlanabilecekleri şekliyle ele alırlar.
R’daki modelleme fonksiyonlarının bir çoğu, formüllerden fonksiyonlara doğru standart bir dönüşüm kullanırlar. Zaten daha önce basit bir dönüşüm görmüştünüz: y ~ x, y = a_1 + a_2 * x’e çevrilmişti. R’ın gerçekte ne yaptığını görmek istiyorsanız, model_matrix () fonksiyonunu kullanabilirsiniz. Bu fonksiyon; bir veri tablosu ve bir formül alarak model denklemini tanımlayan bir tibble çıktısı verir: çıktıdaki her sütun modeldeki bir katsayı ile ilişkilendirilir, fonksiyon her zaman y = a_1 * out1 + a_2 * out_2 şeklindedir. En basit y ~ x1 durumu için bu bize ilginç bir şey sunmaktadır:
df <- tribble(
~y, ~x1, ~x2,
4, 2, 5,
5, 1, 6
)
model_matrix(df, y ~ x1)
#> # A tibble: 2 × 2
#> `(Intercept)` x1
#> <dbl> <dbl>
#> 1 1 2
#> 2 1 1R’ın kesişimi modele ekleme yöntemi, yalnızca bunlarla dolu bir sütuna sahip olmasından ileri gelmektedir. Varsayılan olarak R her zaman bu sütunu ekleyecektir. Şayet istemiyorsanız açıkca -1 olarak ifade etmeniz gerekmektedir:
model_matrix(df, y ~ x1 - 1)
#> # A tibble: 2 × 1
#> x1
#> <dbl>
#> 1 2
#> 2 1Modele daha fazla değişken eklediğinizde, model matrisi de büyüyecektir:
model_matrix(df, y ~ x1 + x2)
#> # A tibble: 2 × 3
#> `(Intercept)` x1 x2
#> <dbl> <dbl> <dbl>
#> 1 1 2 5
#> 2 1 1 6Bu formül gösterimi bazen “Wilkinson-Rogers notasyonu” şeklinde adlandırılır ve başlangıçta Varyans Analizi için Faktöryel Modellerin Sembolik Tanımı bölümünde G. N. Wilkinson ve C. E. Rogers https://www.jstor.org/stable/2346786 tarafından açıklanmıştır. Modelleme cebirinin tüm ayrıntılarını anlamak istiyorsanız, orijinal makaleyi ayrıntılı incelemeye değer.
Aşağıdaki bölümlerde, bu formül gösteriminin kategorik değişkenler, etkileşimler ve dönüşümler için nasıl çalıştığı açıklanmaktadır.
23.4.1 Kategorik değişkenler
Tahminler sürekli olduğunda bir formülden bir fonksiyon üretmek kolaydır, ancak kategorik olduğunda işler biraz daha karmaşık hale gelir. Cinsiyetin -erkek ya da kadın olabilir- y~cinsiyet şeklinde bir formül olduğunu düşünün. Cinsiyet bir sayı olmadığı için y = x_0 + x_1 * cinsiyet gibi bir formüle dönüştürmek mantıklı değildir - sonuçta cinsiyetleri çarpamazsınız! Bunun yerine, R’ın yaptığı şey onu y = x_0 + x_1 * cinsiyet_erkek’e dönüştürmektir, elbette eğer cinsiyet erkek ise cinsiyet_erkek değeri birdir, değilse sıfır olacaktır:
df <- tribble(
~ cinsiyet, ~ yanit,
"erkek", 1,
"kadın", 2,
"erkek", 1
)
model_matrix(df, yanit ~ cinsiyet)
#> # A tibble: 3 × 2
#> `(Intercept)` cinsiyetkadın
#> <dbl> <dbl>
#> 1 1 0
#> 2 1 1
#> 3 1 0R’ın neden cinsiyetkadin sütunu oluşturmadığını merak etmiş olabilirsiniz. Buradaki sorun, diğer sütunlara dayanarak tam olarak tahmin edilebilir bir sütun oluşturmaktır (örn; cinsiyetkadin = 1 - cinsiyeterkek). Ne yazık ki, bunun neden bir problem olduğunun tam detayları bu kitabın kapsamı dışındadır, fakat temelde çok esnek bir model ailesi oluşturmaktadır ve verilere eşit derecede yakın olan sonsuz sayıda model üretilecektir.
Neyse ki, yordayıcı değişkenlerin görselleştirilmesi üzerine odaklanırsanız, kesin parametreleştirme konusunda endişelenmenize gerek yoktur. Bunu somutlaştırmak için bazı verilere ve modellere bakalım. İşte modelr’den sim2 veri kümesi:
ggplot(sim2) +
geom_point(aes(x, y))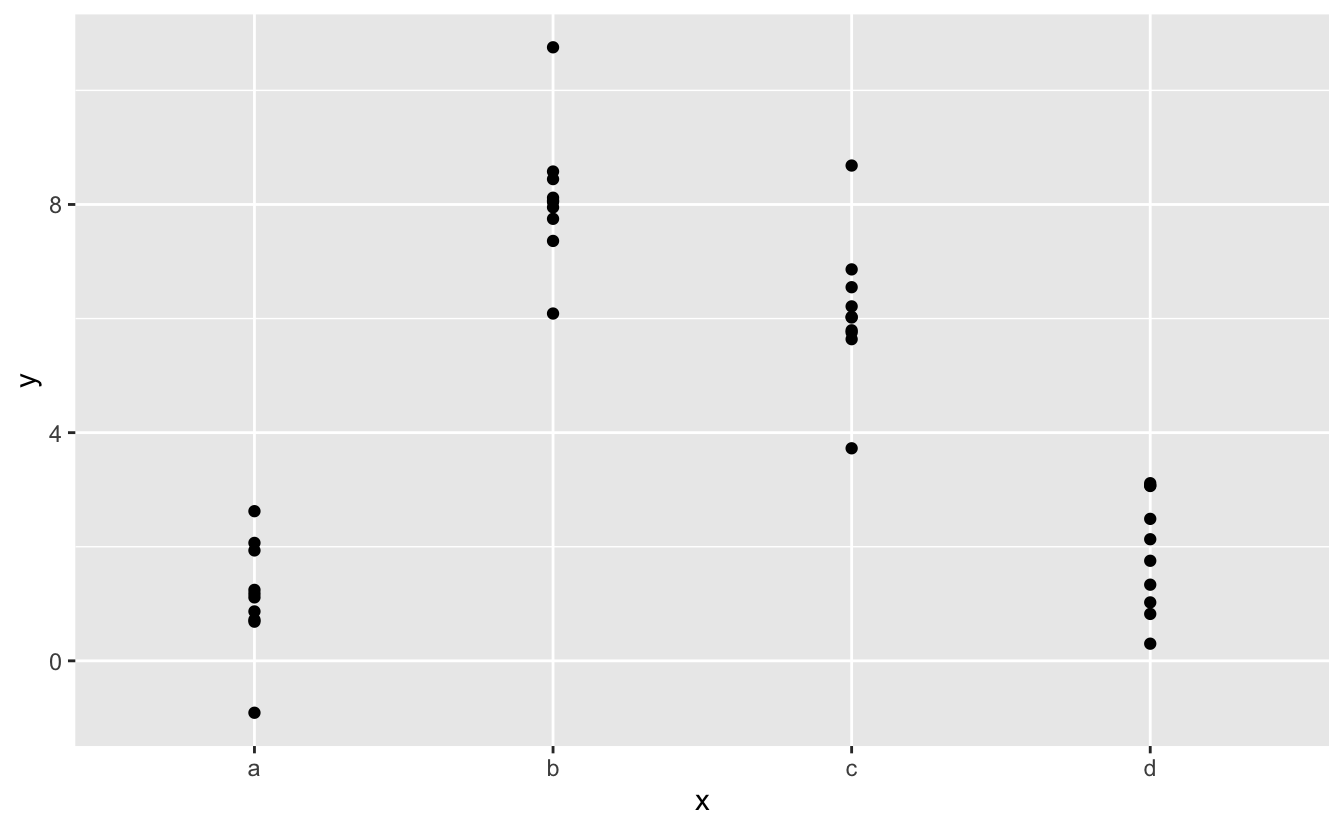
Bir model uygulayabilir ve tahminler üretebiliriz:
mod2 <- lm(y ~ x, data = sim2)
grid <- sim2 %>%
data_grid(x) %>%
add_predictions(mod2)
grid
#> # A tibble: 4 × 2
#> x pred
#> <chr> <dbl>
#> 1 a 1.15
#> 2 b 8.12
#> 3 c 6.13
#> 4 d 1.91Etkisel olarak, kategorik x değerine sahip bir model, her kategori için ortalama değerini öngörecektir. (Neden? Çünkü ortalama, kök-ortalama-kare uzaklığını minimize edecektir.) Yordayıcıları orjinal verilerin üstüne yerleştirirsek bunu görmek kolay olacaktır:
ggplot(sim2, aes(x)) +
geom_point(aes(y = y)) +
geom_point(data = grid, aes(y = pred), colour = "red", size = 4)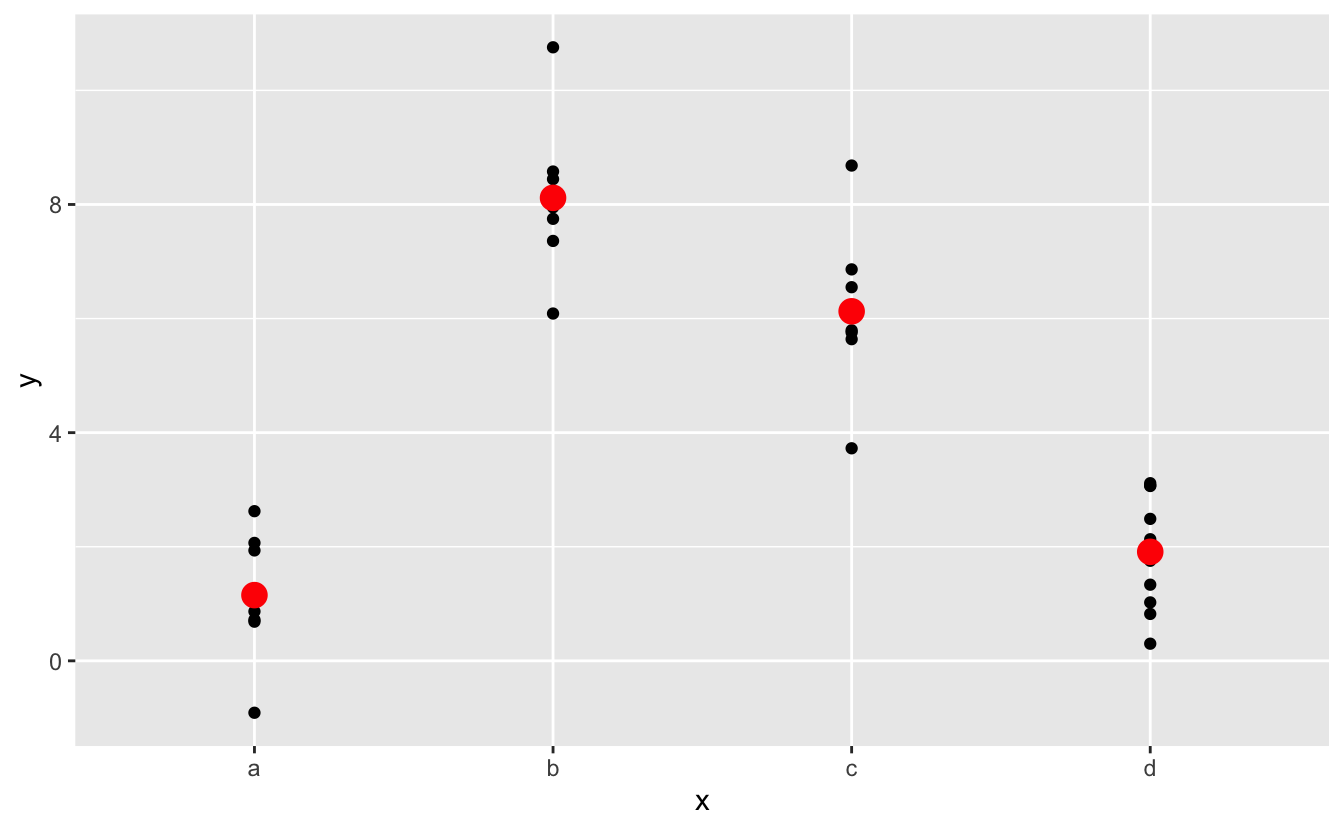
Gözlemleyemediğiniz seviyeler hakkında tahminlerde bulunamazsınız. Bazen bunu kazara yaparsınız diye bu hata mesajını hatırlıyor olmanız faydanıza olacaktır:
tibble(x = "e") %>%
add_predictions(mod2)
#> Error in model.frame.default(Terms, newdata, na.action = na.action, xlev = object$xlevels): factor x has new level e23.4.2 Etkileşimler (sürekli ve kategorik)
Sürekli ve kategorik bir değişkeni birleştirdiğinizde ne olur? sim3 hem kategorik, hem de sürekli bir tahmin içermektedir. Basit bir grafik ile görselleştirebiliriz:
ggplot(sim3, aes(x1, y)) +
geom_point(aes(colour = x2))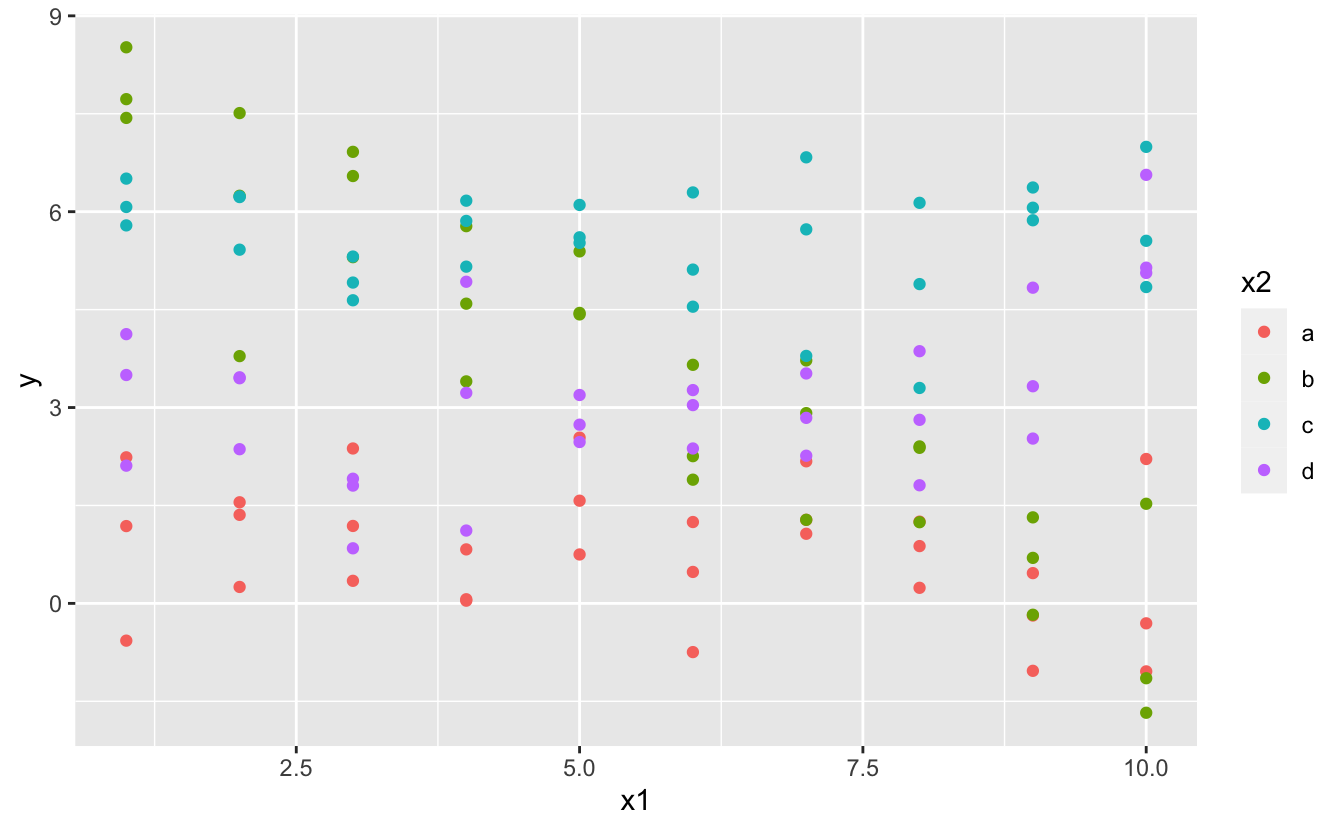
Bu verilere uyarlayabileceğiniz iki olası model bulunmaktadır:
mod1 <- lm(y ~ x1 + x2, data = sim3)
mod2 <- lm(y ~ x1 * x2, data = sim3)Değişkenleri + ile eklediğinizde, model her bir efekti diğerlerinden bağımsız olarak tahmin eder. * ile sözde etkileşim dediğimiz şekilde uyarlamak da mümkündür. Örneğin, y ~ x1 * x2, y = a_0 + a_1 * x1 + a_2 * x2 + a_12 * x1 * x2’ye çevrilir. Ne zaman * kullanırsanız, hem etkileşimin hem de bileşenlerin modele dahil edildiğine dikkat edin.
Bu modelleri görselleştirmek için iki yeni numaraya ihtiyacımız var:
İki tahminimiz bulunmaktadır, bu yüzden her iki değişkene de
data_grid()uygulamamız gerekiyor. Bu tümx1vex2’ye ait tüm benzersiz değerleri bulur ve ardından tüm kombinasyonları oluşturur.Her iki modelden de aynı anda yordayıcılar üretmek için her tahmini satır olarak ekleyen
gather_predictions ()yöntemini kullanabiliriz.gather_predictions ()‘nin tamamlayıcısı, her bir tahmini yeni bir sütuna ekleyenspread_predictions ()’ dır.
Birlikte bize bunu verirler:
grid <- sim3 %>%
data_grid(x1, x2) %>%
gather_predictions(mod1, mod2)
grid
#> # A tibble: 80 × 4
#> model x1 x2 pred
#> <chr> <int> <fct> <dbl>
#> 1 mod1 1 a 1.67
#> 2 mod1 1 b 4.56
#> 3 mod1 1 c 6.48
#> 4 mod1 1 d 4.03
#> 5 mod1 2 a 1.48
#> 6 mod1 2 b 4.37
#> # … with 74 more rowsHer iki modelin sonuçlarını fasetleyerek(?) tek bir grafik üzerinde görselleştirebiliriz:
ggplot(sim3, aes(x1, y, colour = x2)) +
geom_point() +
geom_line(data = grid, aes(y = pred)) +
facet_wrap(~ model)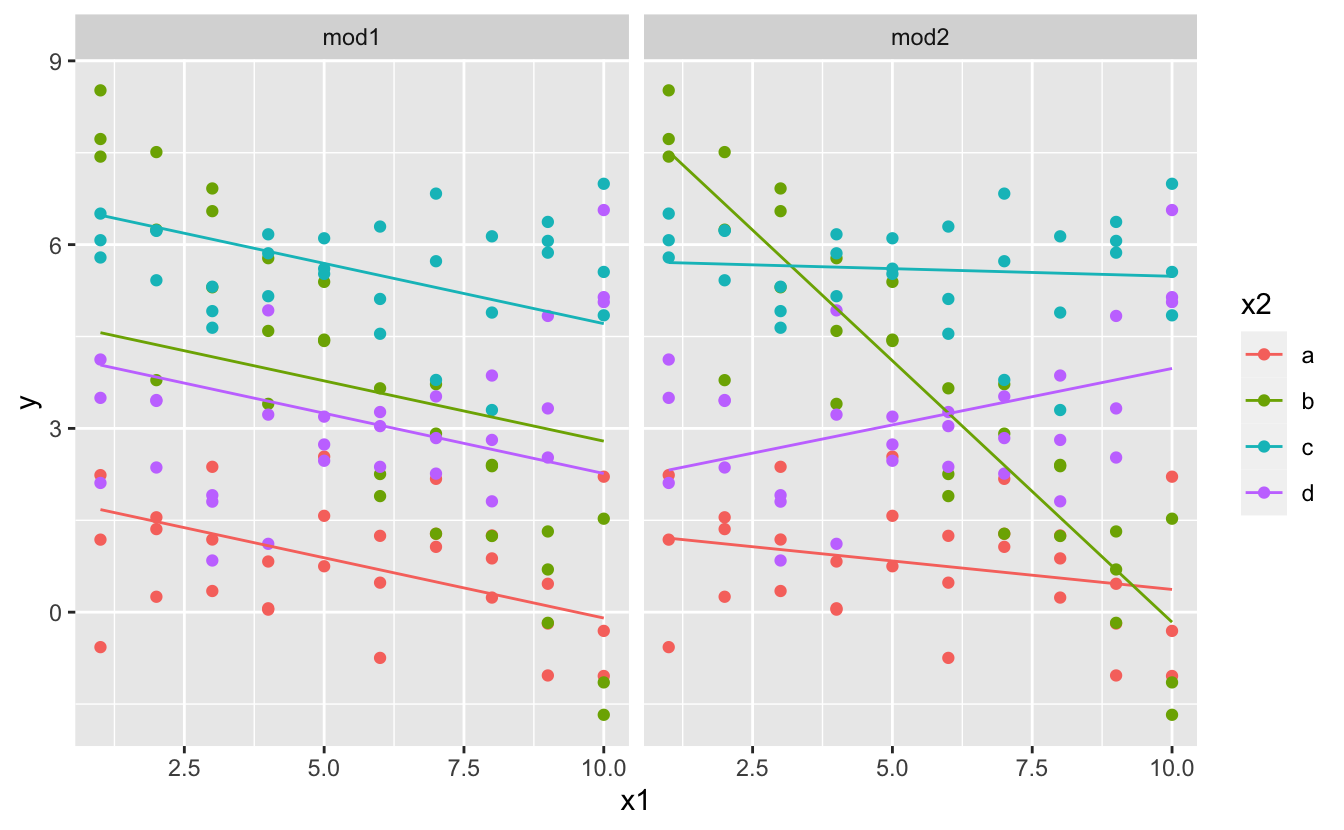
+ kullanan modelin her doğru için aynı eğime sahip ancak farklı etkileşimler olduklarına dikkat ediniz. * kullanan model, her bir doğru için farklı bir eğime ve etkileşime sahiptir.
Bu veriler için hangi model daha iyidir? Artıklara bakabiliriz. Burada hem model, hem de x2 tarafından fasetlenmiş(?) durumdayım, çünkü her gruba ait kalıbı görmek daha kolay.
sim3 <- sim3 %>%
gather_residuals(mod1, mod2)
ggplot(sim3, aes(x1, resid, colour = x2)) +
geom_point() +
facet_grid(model ~ x2)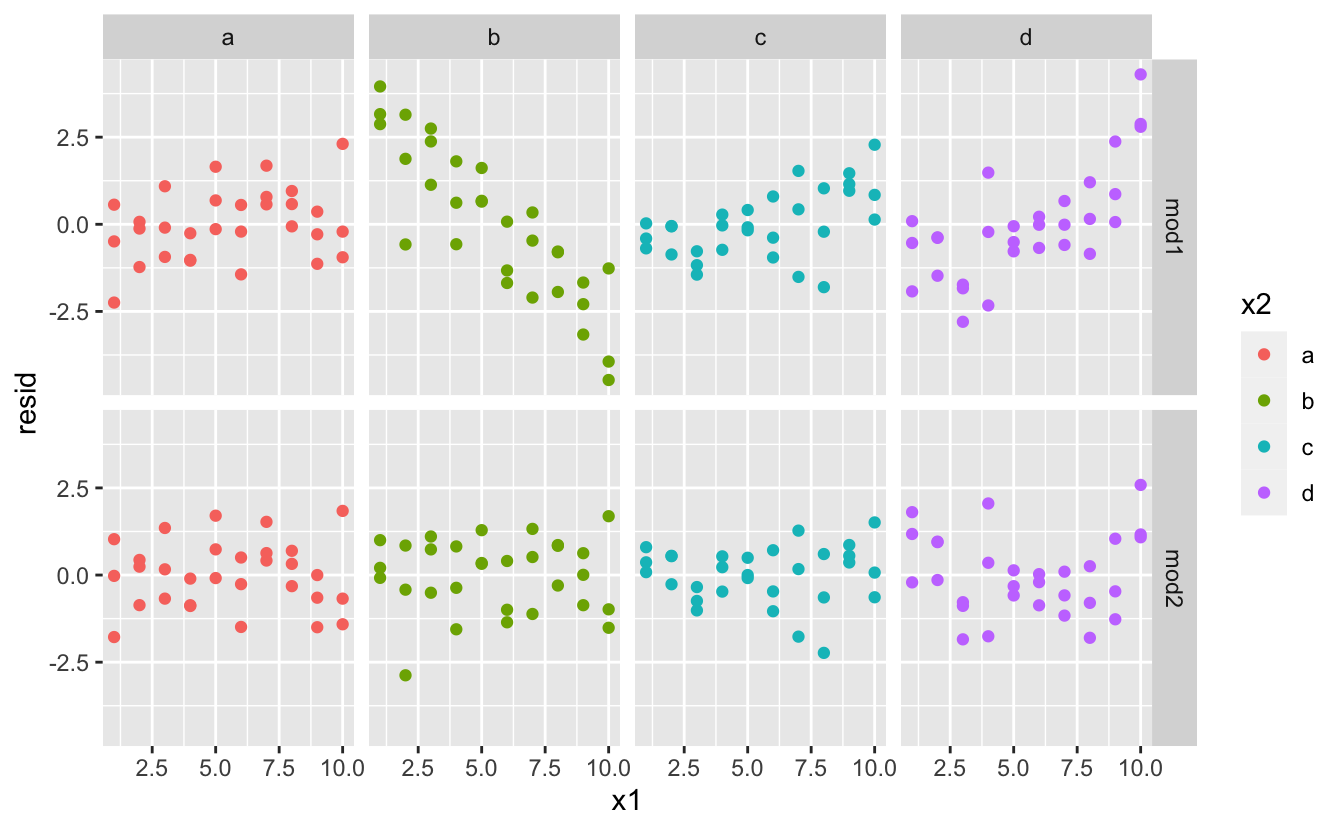
mod2 açısından artıklarda çok belirgin olmayan bir örüntü görülmektedir. mod1 açısından artıklar b’de modelin bazı örüntüleri açıkca kaçırdığını ancak yine de c ve d’de örüntülerin olduğunu göstermektedir. mod1 veya mod2’nin hangisinin daha iyi olduğunu söylemenin kesin bir yolu olup olmadığını merak edebilirsiniz. Vardır, ancak çok fazla matematiksel altyapı gerektirmektedir ve gerçekten şu an konumuz bu değil. Burada, modelin ilgilendiğimiz kalıbı yakalayıp yakalamadığına dair kalitatif bir değerlendirme yapmak istiyoruz.
23.4.3 Etkileşimler (iki sürekli arasında)
İki sürekli değişken için eşdeğer modele bakalım. Başlangıçta işler önceki örnekle neredeyse aynı şekilde devam eder:
mod1 <- lm(y ~ x1 + x2, data = sim4)
mod2 <- lm(y ~ x1 * x2, data = sim4)
grid <- sim4 %>%
data_grid(
x1 = seq_range(x1, 5),
x2 = seq_range(x2, 5)
) %>%
gather_predictions(mod1, mod2)
grid
#> # A tibble: 50 × 4
#> model x1 x2 pred
#> <chr> <dbl> <dbl> <dbl>
#> 1 mod1 -1 -1 0.996
#> 2 mod1 -1 -0.5 -0.395
#> 3 mod1 -1 0 -1.79
#> 4 mod1 -1 0.5 -3.18
#> 5 mod1 -1 1 -4.57
#> 6 mod1 -0.5 -1 1.91
#> # … with 44 more rowsdata_grid() içinde seq_range() kullanımına dikkat edin. Her seferinde benzersiz x değerini kullanmak yerine, minimum ve maksimum sayılar arasında düzenli aralıklarla beş değerlik bir ızgara kullanacağım. Muhtemelen burada çok önemli değil, ancak genel olarak yararlı bir tekniktir. seq_range() için iki tane daha faydalı argüman bulunmaktadır:
pretty = TRUE, “hoş” bir sekans yaratacaktır, yani insan gözüne hoş görünen birşey diyebiliriz. Çıktı tabloları üretmek istiyorsanız bu yöntem kullanışlıdır:seq_range(c(0.0123, 0.923423), n = 5) #> [1] 0.0123 0.2401 0.4679 0.6956 0.9234 seq_range(c(0.0123, 0.923423), n = 5, pretty = TRUE) #> [1] 0.0 0.2 0.4 0.6 0.8 1.0trim = 0.1, kuyruk değerlerinin %10’nunu keser. Değişkenler uzun kuyruklu bir dağılıma sahipse ve merkeze yakın değerler oluşturmaya odaklanmak istiyorsanız, bu yöntem kullanışlıdır:x1 <- rcauchy(100) seq_range(x1, n = 5) #> [1] -115.9 -83.5 -51.2 -18.8 13.5 seq_range(x1, n = 5, trim = 0.10) #> [1] -13.84 -8.71 -3.58 1.55 6.68 seq_range(x1, n = 5, trim = 0.25) #> [1] -2.1735 -1.0594 0.0547 1.1687 2.2828 seq_range(x1, n = 5, trim = 0.50) #> [1] -0.725 -0.268 0.189 0.647 1.104expand = 0.1, bir anlamda,trim()’in tam tersi şekilde, aralığı %10 genişletir.x2 <- c(0, 1) seq_range(x2, n = 5) #> [1] 0.00 0.25 0.50 0.75 1.00 seq_range(x2, n = 5, expand = 0.10) #> [1] -0.050 0.225 0.500 0.775 1.050 seq_range(x2, n = 5, expand = 0.25) #> [1] -0.125 0.188 0.500 0.812 1.125 seq_range(x2, n = 5, expand = 0.50) #> [1] -0.250 0.125 0.500 0.875 1.250
Şimdi bu modeli deneyelim ve görselleştirelim. İki sürekli tahminimiz var, böylece modeli bir 3B yüzey gibi hayal edebilirsiniz. geom_tile() kullanarak şunu gösterebiliriz:
ggplot(grid, aes(x1, x2)) +
geom_tile(aes(fill = pred)) +
facet_wrap(~ model)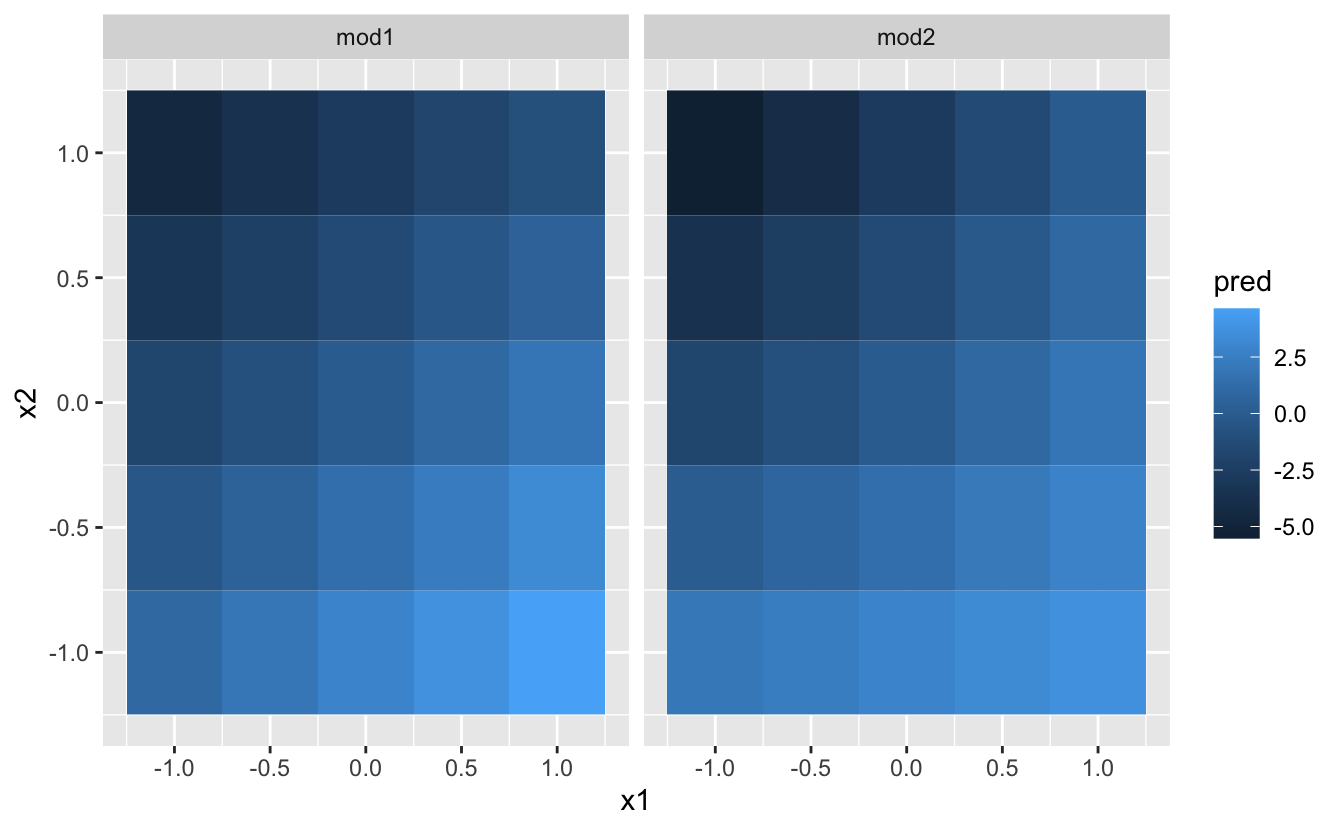
Bu durum, modellerin çok farklı olmadığını gösteriyor! Ancak bu kısmen bir yanılsamadır: gözlerimiz ve beyinlerimiz renk tonlarını doğru şekilde karşılaştırmakta çok iyi değillerdir. Yüzeye üstten bakmak yerine, her iki taraftan da birden çok dilim göstererek bakabiliriz:
ggplot(grid, aes(x1, pred, colour = x2, group = x2)) +
geom_line() +
facet_wrap(~ model)
ggplot(grid, aes(x2, pred, colour = x1, group = x1)) +
geom_line() +
facet_wrap(~ model)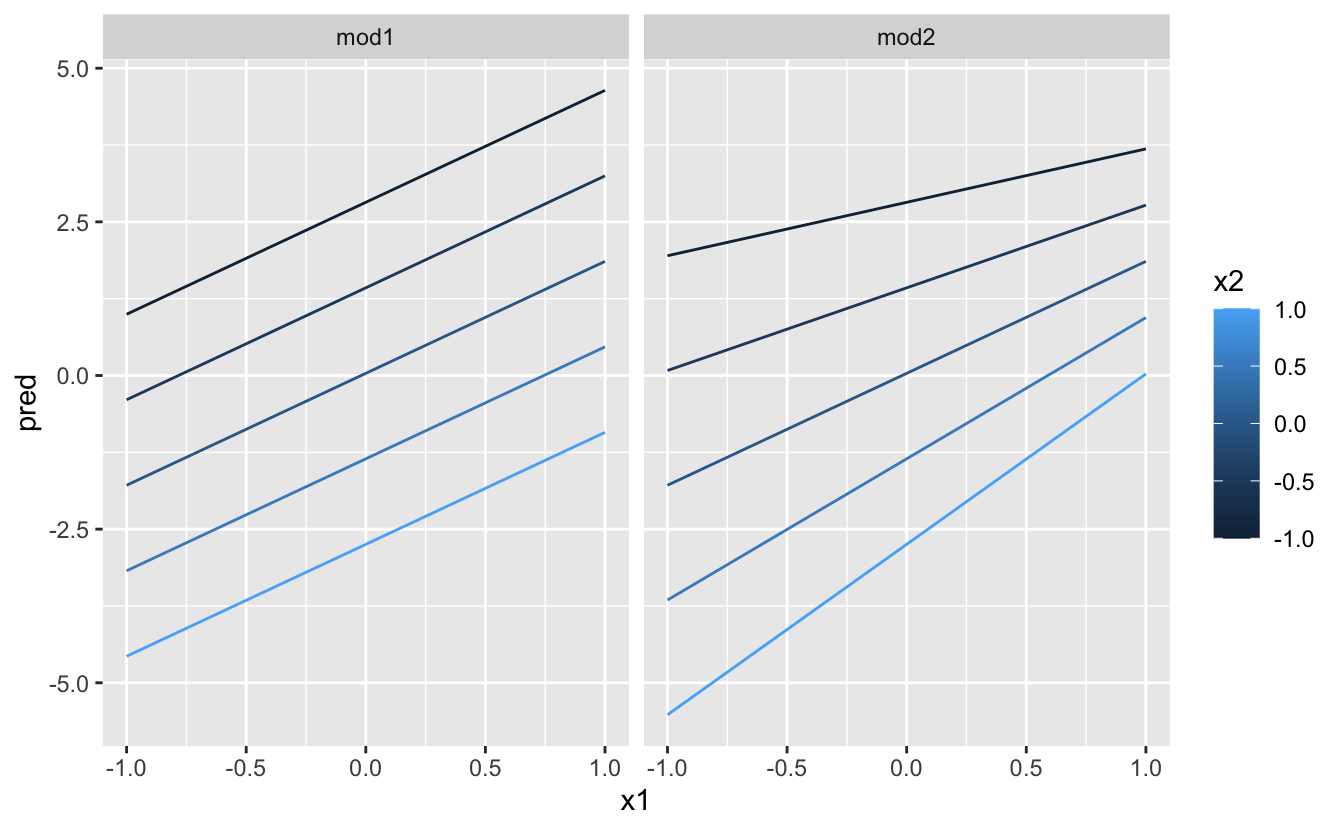
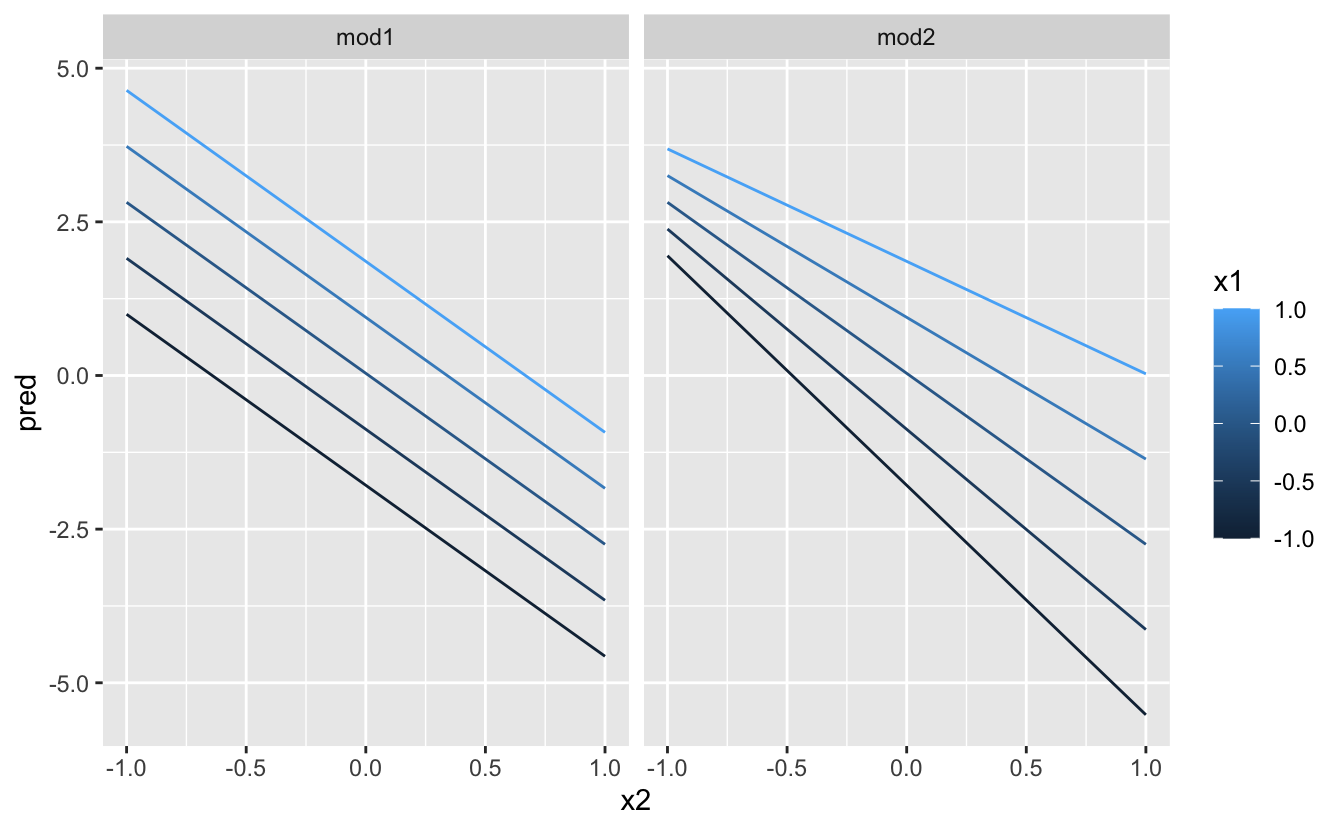
Bu, iki sürekli değişken arasındaki etkileşimin temelde kategorik ve sürekli bir değişkenle aynı şekilde çalıştığını gösterir. Etkileşimlerden biri, sabit bir denge olmadığını söylüyor: y’yi tahmin etmek için aynı anda hem x1 hem de x2 değerlerini göz önünde bulundurmanız gerekir.
Sadece iki değişkenle bile, başarılı bir görsel yakalamak zordur. Ancak bunun sebepleri mevcuttur: Üç veya daha fazla değişkenin aynı anda nasıl etkileşime girdiğini anlamanın kolay olacağı elbette beklenemez! Fakat yine de biraz tasarruf ettik, çünkü keşfetmek için modeller kullanıyoruz ve modelinizi zaman içinde kademeli olarak geliştirebilirsiniz. Modelin mükemmel olması gerekmiyor, yalnızca verileriniz hakkında biraz daha bilgi vermesi, yardımcı olması gerekiyor.
mod2’nin mod1’den daha iyisini yapıp yapmadığını anlamak için artıkları incelemek üzere biraz zaman harcadım. Sanırım öyle, ama yeterli değil. Uygulamalar kısmında üzerinde çalışmak için fırsatınız olacak.
23.4.4 Dönüşümler
Model formülü içinde de dönüşümler gerçekleştirebilirsiniz. Örneğin, log(y) ~ sqrt(x1) + x2, log(y) = a_1 + a_2 * sqrt(x1) + a_3 * x2’ye dönüştürülebilir. Dönüşüm +, *, ^ veya - içeriyorsa, onu I() içine almanız gerekir. Böylece R, modelin teknik özelliklerinin bir parçası gibi davranmaz. Örneğin y ~ x + I(x ^ 2), y = a_1 + a_2 * x + a_3 * x^2’ye çevrilir. Eğer I()’yı unutur ve y ~ x ^ 2 + x şeklinde belirtirseniz, R y ~ x * x + x’i hesaplar. x * x, x’in kendiyle etkileşimi demektir ki bu da x ile aynı demektir. R, gereksiz değişkenleri otomatik olarak işleme almaz, böylece x+x, x olur, yani y ~ x ^ 2 + x, y = a_1 + a_2 * x fonskiyonunu belirtmektedir. Muhtemelen istediğiniz bu değildir!
Yine de, modelinizin ne yaptığı hakkında kafanız karışırsa, tam olarak hangi lm() denkleminin uygun olduğunu görmek için model_matrix() yöntemini kullanabilirsiniz:
df <- tribble(
~y, ~x,
1, 1,
2, 2,
3, 3
)
model_matrix(df, y ~ x^2 + x)
#> # A tibble: 3 × 2
#> `(Intercept)` x
#> <dbl> <dbl>
#> 1 1 1
#> 2 1 2
#> 3 1 3
model_matrix(df, y ~ I(x^2) + x)
#> # A tibble: 3 × 3
#> `(Intercept)` `I(x^2)` x
#> <dbl> <dbl> <dbl>
#> 1 1 1 1
#> 2 1 4 2
#> 3 1 9 3Dönüşümler kullanışlıdır, çünkü doğrusal olmayan fonksiyonlara benzetmek için de kullanabilirsiniz. Eğer matematik dersi almışsanız, Taylor’un teoremini duymuş olma ihtimaliniz vardır ki, sonsuz miktarda polinomla herhangi bir düzgün fonksiyona yaklaşabilirsiniz. Bu, y = a_1 + a_2 * x + a_3 * x^2 + a_4 * x ^ 3 gibi bir denklemi kullanarak keyfi bir şekilde düzgün bir fonksiyona yakınlaşmak için polinom işlevini kullanabileceğiniz anlamına gelmektedir. Bu diziyi elle yazmak sıkıcı olacağından, R yardımcı bir fonksiyon sağlar: poly():
model_matrix(df, y ~ poly(x, 2))
#> # A tibble: 3 × 3
#> `(Intercept)` `poly(x, 2)1` `poly(x, 2)2`
#> <dbl> <dbl> <dbl>
#> 1 1 -7.07e- 1 0.408
#> 2 1 -7.85e-17 -0.816
#> 3 1 7.07e- 1 0.408Bununla beraber, poly()’nin kullanımıyla ilgili büyük bir sıkıntı vardır: veri aralığının dışında, polinomlar hızla pozitif ya da negatif sonsuzluğa kaçarlar. Diğer bir güvenli alternatif splines::ns() kullanmaktır.
library(splines)
model_matrix(df, y ~ ns(x, 2))
#> # A tibble: 3 × 3
#> `(Intercept)` `ns(x, 2)1` `ns(x, 2)2`
#> <dbl> <dbl> <dbl>
#> 1 1 0 0
#> 2 1 0.566 -0.211
#> 3 1 0.344 0.771Doğrusal olmayan bir fonksiyon üzerinde çalışırken yaklaşık olarak nasıl göründüğünü görelim:
sim5 <- tibble(
x = seq(0, 3.5 * pi, length = 50),
y = 4 * sin(x) + rnorm(length(x))
)
ggplot(sim5, aes(x, y)) +
geom_point()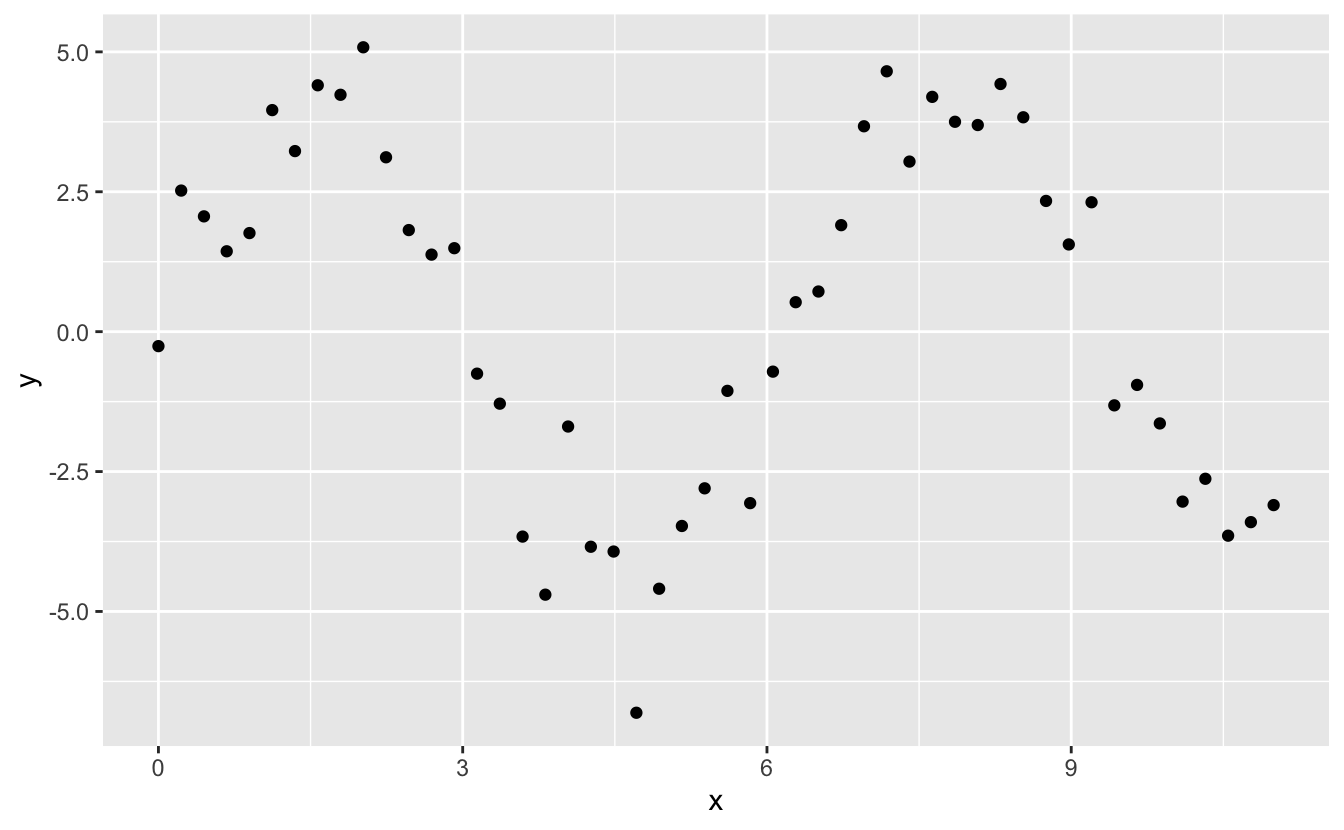
Bu verilere, beş model uygulayacağım.
mod1 <- lm(y ~ ns(x, 1), data = sim5)
mod2 <- lm(y ~ ns(x, 2), data = sim5)
mod3 <- lm(y ~ ns(x, 3), data = sim5)
mod4 <- lm(y ~ ns(x, 4), data = sim5)
mod5 <- lm(y ~ ns(x, 5), data = sim5)
grid <- sim5 %>%
data_grid(x = seq_range(x, n = 50, expand = 0.1)) %>%
gather_predictions(mod1, mod2, mod3, mod4, mod5, .pred = "y")
ggplot(sim5, aes(x, y)) +
geom_point() +
geom_line(data = grid, colour = "red") +
facet_wrap(~ model)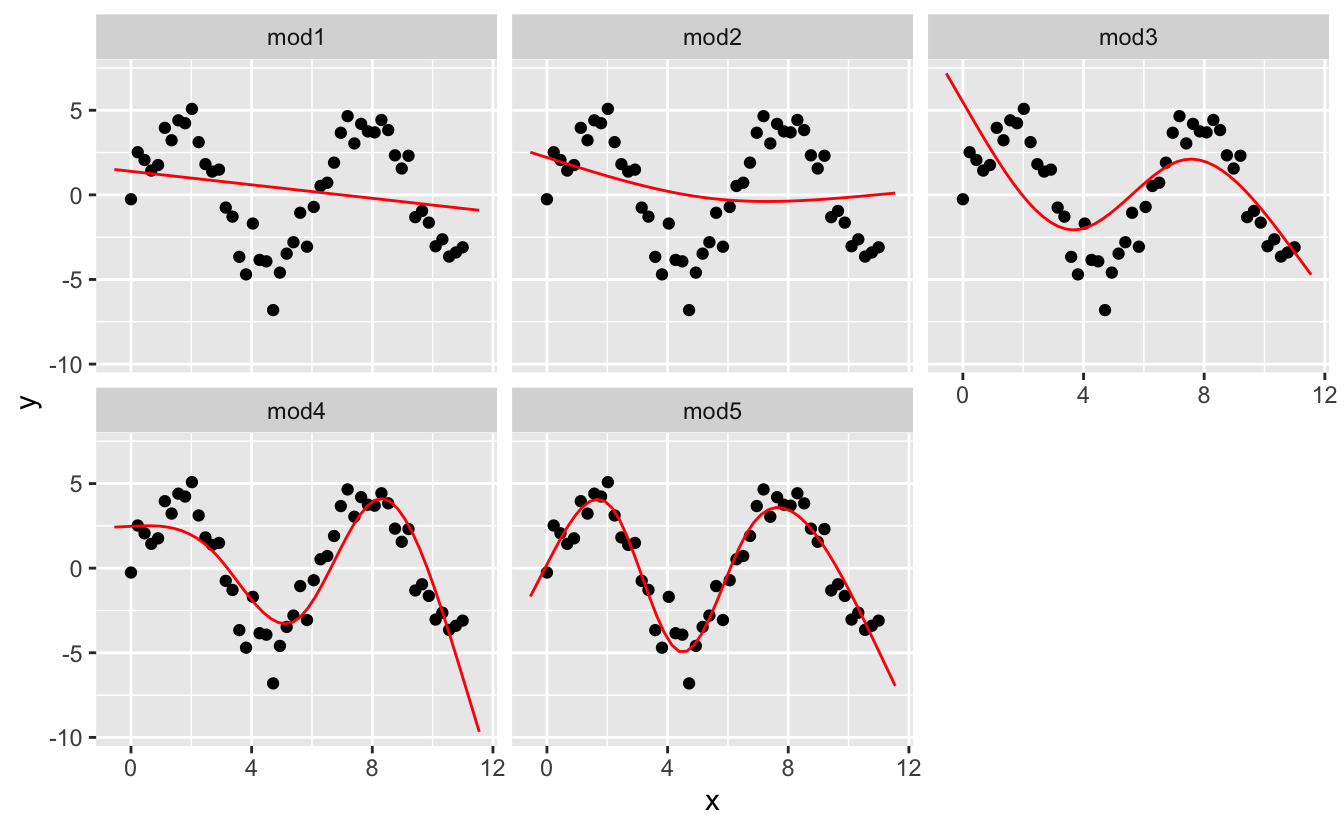
Veri aralığının dışında kalan değerin açıkça kötü olduğuna dikkat edin. Bu, bir fonksiyona polinom ile yaklaşmanın olumsuz yanıdır. Ancak bu, her model için gerçekten bir problemdir: Model, veri aralığının dışına çıkmaya başladığınızda, bunun doğru olup olmadığını söyleyemez. Teori ve bilime güvenmelisiniz.
23.4.5 Uygulamalar
Kesişimi (ğntercept) olmayan bir model kullanarak
sim2analizini tekrarlarsanız ne olur? Model denklemi nasıl olur? Tahminlere ne olur?sim3vesim4’e uyguladığım modeller için oluşturulan denklemlerimodel_matrix()kullanarak açıklayın. Neden*kesişim için iyi bir kısayoldur?Temel ilkeleri kullanarak, aşağıdaki iki modeldeki formülleri fonksiyonlara dönüştürün.
(İpucu: kategorik değişkeni 0-1 değişkene dönüştürerek başlayın.)mod1 <- lm(y ~ x1 + x2, data = sim3) mod2 <- lm(y ~ x1 * x2, data = sim3)mod1vemod2’den hangisisim4için daha iyidir?mod2’nin örüntüleri ortadan kaldırmak için daha hassas bir şekilde, biraz daha iyi bir iş çıkardığını düşünüyorum. Görüşümü destekleyen bir grafik çizdirebilir misiniz?
23.5 Kayıp değerler
Kayıp değerler açıkça değişkenler arasındaki ilişki hakkında herhangi bir bilgi iletemez, bu nedenle modelleme fonksiyonları kayıp değerler içeren satırları yok sayar. R varsayılan olarak uyarı vermeden bu işlemi gerçekleştirir, ancak seçeneklere göre (na.action = na.warn) (önkoşullarda çalıştırın), bir uyarı almanız sağlanabilir.
df <- tribble(
~x, ~y,
1, 2.2,
2, NA,
3, 3.5,
4, 8.3,
NA, 10
)
mod <- lm(y ~ x, data = df)
#> Warning: Dropping 2 rows with missing valuesUyarıyı engellemek için, na.action = na.exclude şeklinde ayarlamalısınız.
mod <- lm(y ~ x, data = df, na.action = na.exclude)nobs() ile kullanılan gözlem sayılarını görebilirsiniz:
nobs(mod)
#> [1] 323.6 Diğer model aileleri
Bu bölüm özellikle y = a_1 * x1 + a_2 * x2 + ... + a_n * xn formunun ilişkisini varsayan doğrusal modeller sınıfına odaklanmıştır. İlaveten, doğrusal modeller artıkların normal dağılım gösterdikleri varsayarlar ki bunun hakkında henüz konuşmadık. Doğrusal modeli çeşitli ilginç şekillerde genişleten çok sayıda model sınıfı vardır. Onlardan bazıları:
Genelleştirilmiş Doğrusal Modeller (GLM), örn;
stats::glm(). Doğrusal modeller, tepkinin sürekli olduğunu ve hatanın normal bir dağılıma sahip olduğunu varsaymaktadır. Genelleştirilmiş doğrusal modeller, sürekli olmayan yanıtları (örneğin ikili veri veya sayıları) içerecek şekilde doğrusal modelleri genişletir. İstatistiksel olabilirlik fikrine dayanan bir mesafe ölçümü tanımlayarak çalışırlar.Genelleştirilmiş Eklemeli Modeller (GAM)_, örn;
mgcv::gam(). Genelleştirilmiş doğrusal modeller ile keyfi olarak düzgün fonksiyonların birlikte çalışmasını sağlar.Penalize Doğrusal Modeller (PLM), örn;
glmnet::glmnet(). Karmaşık modellerin penalize uzaklığa bir penaltı terimi ekler (parametre vektörü ile orijin arasındaki mesafe ile tanımlandığı şekilde). Bu, aynı popülasyondaki yeni veri setleri için daha iyi genelleştirme modelleri yapma eğilimindedir.Kaba Doğrusal Modeller (RLM), örn;
MASS:rlm(). Çok uzakta olan noktaların ağırlığını aşağı çekmek için aradaki mesafeyi kısaltır. Aykırı değerler olmadığında çok işe yaramasa da, bu onları aykırı değerlere karşı daha az hassas hale getirir.Ağaçlar_, örn;
rpart::rpart(). Doğrusal modellerden tamamen farklı bir şekilde problemi ele alırlar. Verilere aşamalı olarak daha küçük parçalara bölerek, parçalar halinde sabit modele uyarlanırlar. Ağaçlar kendi başlarına çok etkili değillerdir, ancak, random forest gibi modeller (örn;randomForest::randomForest()) veya gradient boosting machine (xgboost::xgboost) tarafından toplu olarak kullanıldığında çok güçlüdürler.
Bu modellerin hepsi programlama açısından benzer şekilde çalışmaktadır. Doğrusal modellerde ustalaştığınızda, benzeri diğer model sınıflarının mekaniklerinde ustalaşmayı da kolay bulabilirsiniz. Yetenekli bir modelci olmak bazı iyi genel prensiplere ve büyük bir teknik araç kutusuna sahip olmak anlamına gelmektedir. Artık bazı genel araçları ve kullanışlı bir model sınıfını öğrendiğinize göre, diğer kaynaklardan daha fazla sınıf öğrenebilir ve devam edebilirsiniz.