24 Model geliştirme
24.1 Giriş
Bir önceki bölümde doğrusal modellerin nasıl çalıştığını ve bir modelin verileriniz hakkında size neler ifade ettiğini anlamanız için bazı temel araçları öğrendiniz. Önceki bölüm, simüle edilmiş veri setlerine odaklanmaktaydı. Bu bölüm, verileri anlamanızda size yardımcı olacak bir modeli nasıl geliştirebileceğinizi gösteren gerçek verilere odaklanacaktır.
Verilerinizi, kalıplara ve artıklara (residuals) ayıran bir model üzerine düşünebiliyor olmanızdan faydalanacağız. Görselleştirme yoluyla kalıpları bulacağız, sonra onları bir model ile kesin ve somut hale getireceğiz. Sonrasında işlemi tekrarlayacağız, ancak eski yanıt değişkenini modeldeki artıklar ile değiştirmeliyiz. Amaç, kafanızı veri içerisindeki örtük bilgilerden çıkartarak, nicel bir modeldeki açık bilgilere yöneltmektir. Bu hem yeni alanların uygulanmasını, hem de başkalarının kullanımını kolaylaştıracaktır.
Bu, çok büyük ve karmaşık veri setleri için oldukça fazla iş yükü demektir. Kesinlikle alternatif yaklaşımlar mevcuttur - daha fazla makina öğrenmesi yaklaşımı, modelin öngörü kabiliyetine basitçe odaklanabilir. Bu yaklaşımlar kara kutular üretme eğilimindedir: Model, tahmin üretmede çok iyi bir iş çıkarabilir, ancak siz nedenini bilmiyor olabilirsiniz. Bu tamamen makul bir yaklaşımdır, ancak bu durum sizin gerçek dünya bilginizi modele uygulamanızı zorlaştırmaktadır. Bu da, sırayla temel değişiklikler olarak, modelin uzun vadede çalışmaya devam edip etmeyeceğini belirlemekte güçlük çıkartmaktadır. Çoğu gerçek model için, bu yaklaşımın bir kombinasyonunu ve daha klasik bir otomatik yaklaşımı kullanmanızı bekliyorum.
Ne zaman duracağınızı bilmek güçtür. Modelinizin ne kadar iyi olduğunu ve daha fazla emek harcamınızın mümkün olmadığını anlamanız gerekir. Reddit kullanıcısı Broseidon241’den gelen bu alıntıyı özellikle beğendim:
Uzun zaman önce sanat dersinde öğretmenim bana şöyle demişti “Bir sanatçının bir eseri ne zaman bitirdiğini bilmesi gerekir. Bir şeyi mükemmel haline getiremezsiniz - o halde bitirin. Eğer beğenmediyseniz, tekrar yapın. Aksi takdirde yeni bir şeye başlayın”. Hayatımın ilerleyen döneminde şöyle bir şey işittim “Kötü bir terzi birçok hata yapar. İyi bir terzi bu hataları düzeltmek için çok çalışır. Harika bir terzi, giysiyi atmaktan ve yeniden başlamaktan korkmaz.”
-Broseidon241, https://www.reddit.com/r/datascience/comments/4irajq
24.1.1 Ön koşullar
Önceki bölümdekiyle aynı araçları kullanacağız, ancak bazı gerçek veri setleri ekleyerek: ggplot2’den diamonds ve nycflights13’den flights. Ayrıca tarih/saat ile ilgili çalışmak için flights içinde yer alan lubridate paketine ihtiyacımız olacak.
library(tidyverse)
library(modelr)
options(na.action = na.warn)
library(nycflights13)
library(lubridate)24.2 Neden düşük kalite elmaslar daha pahalıdır?
Önceki bölümlerde, elmasların kalitesi ve fiyatı arasında şaşırtıcı bir ilişki olduğunu gördük: düşük kalite elmaslar (kötü kesim, kötü renk ve düşük netlik) daha yüksek fiyat demekti.
ggplot(diamonds, aes(cut, price)) + geom_boxplot()
ggplot(diamonds, aes(color, price)) + geom_boxplot()
ggplot(diamonds, aes(clarity, price)) + geom_boxplot()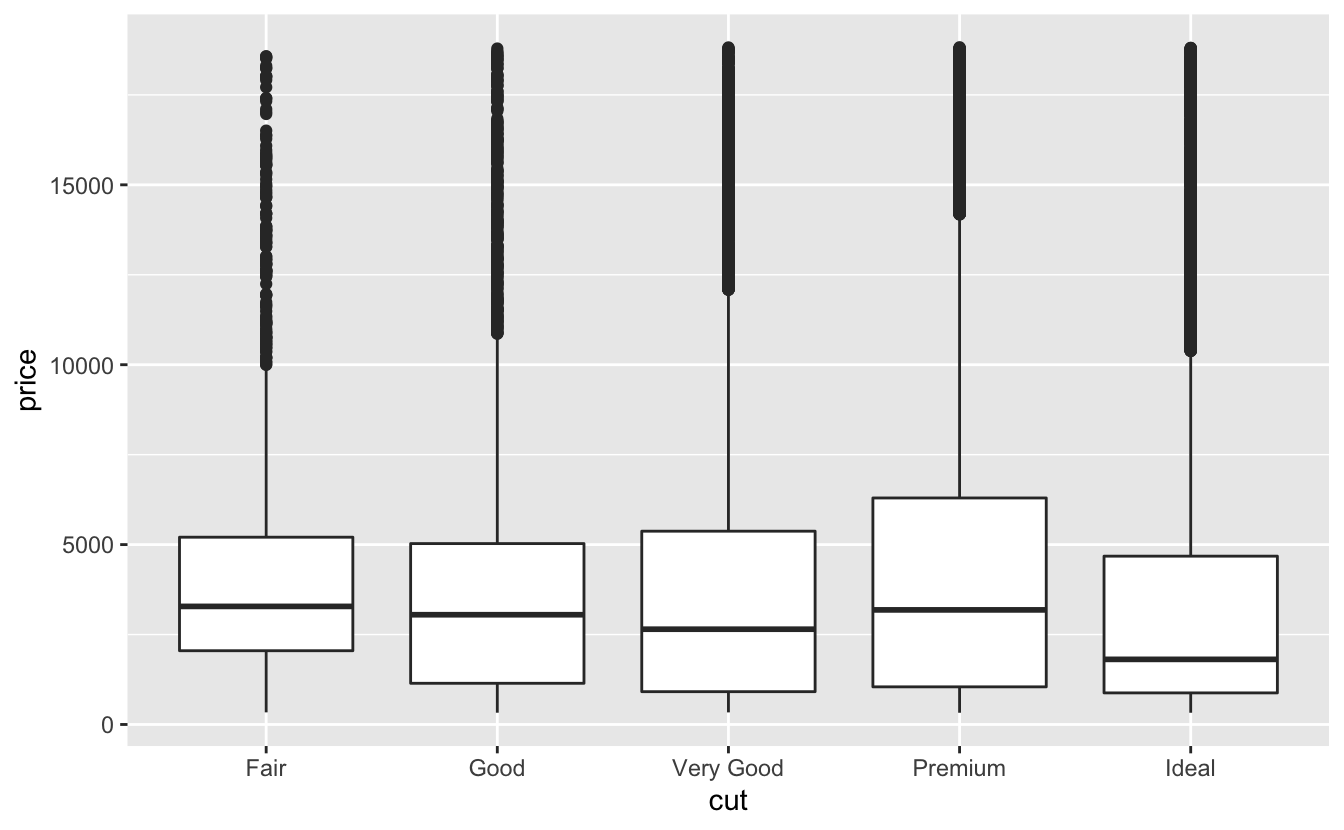
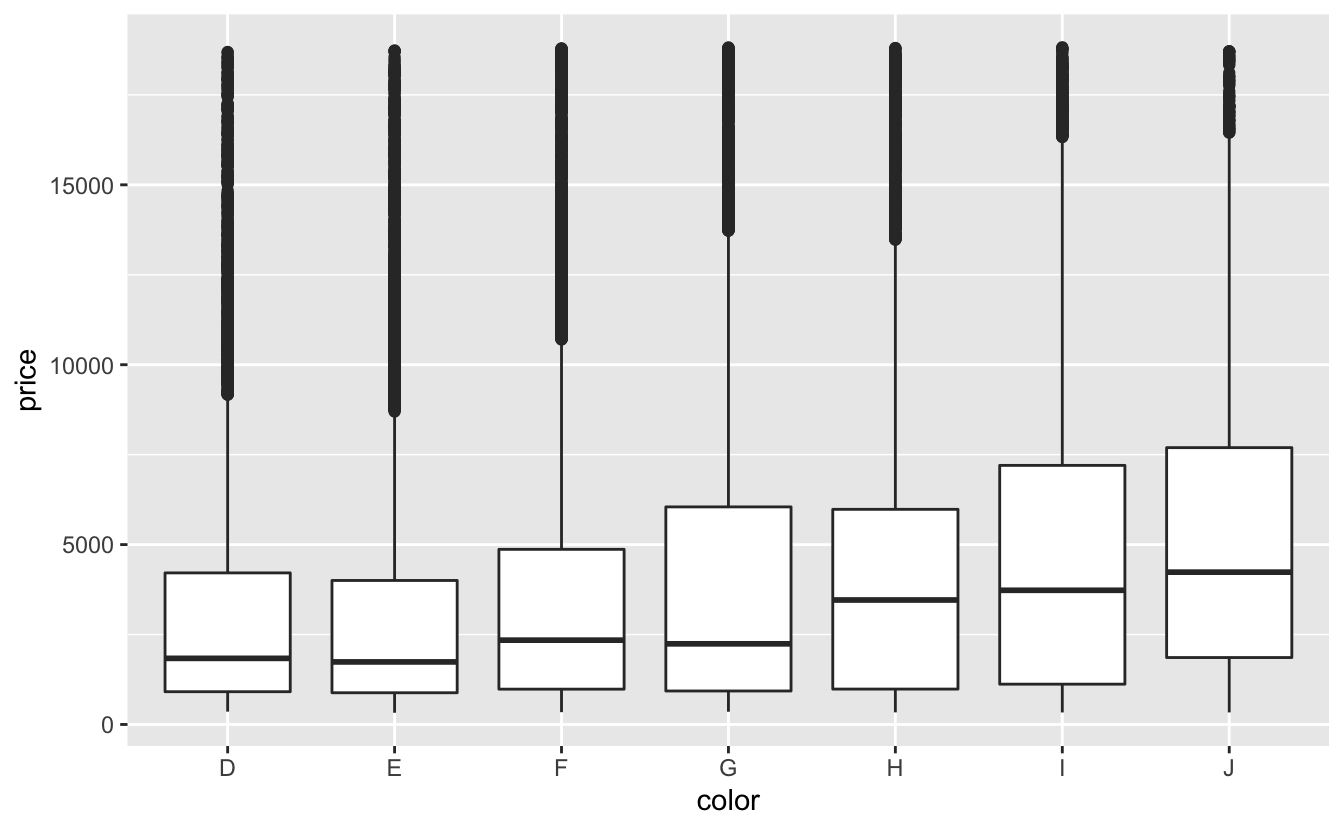
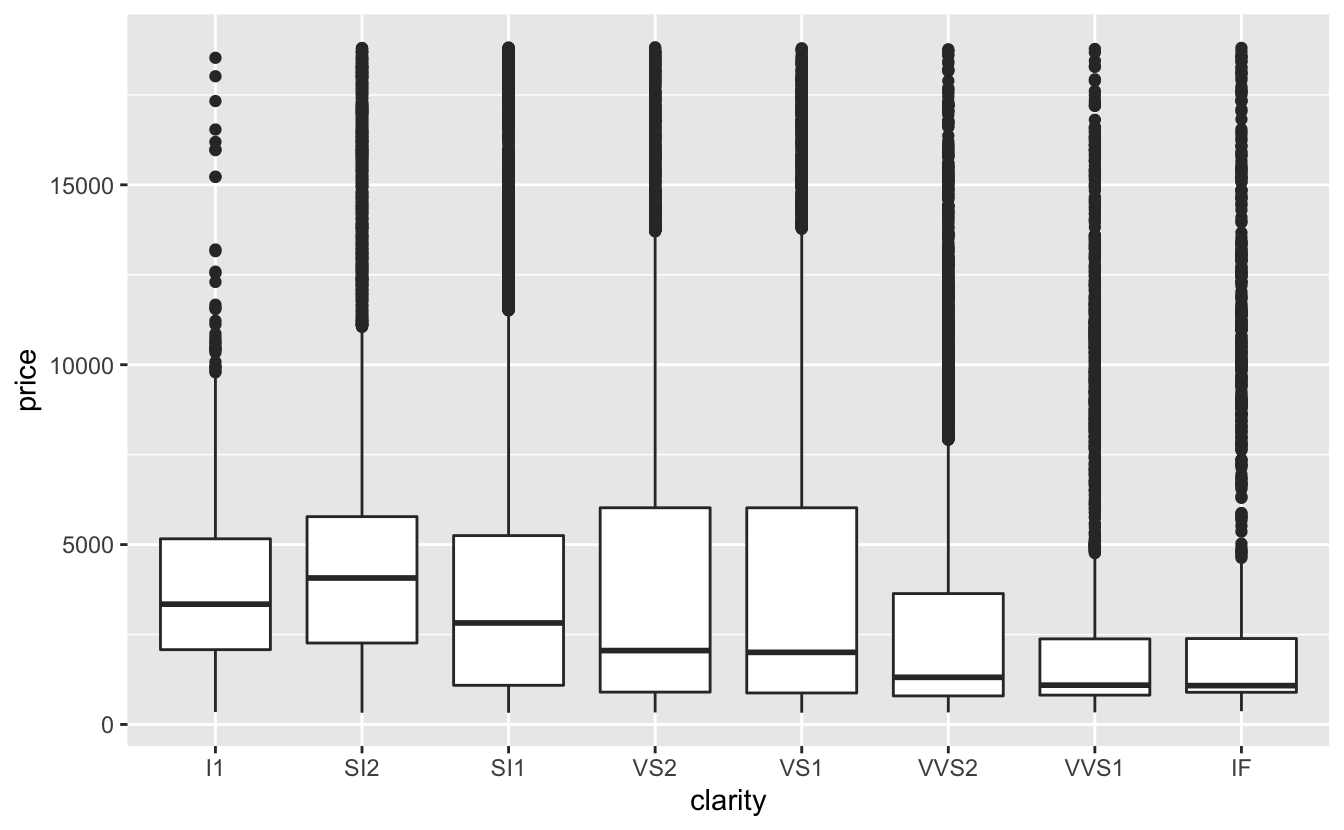
En kötü elmas renginin J (hafif sarı) ve en kötü netliğin I1 (çıplak gözle görülebilen kapanımlar) olduğunu unutmayın.
24.2.1 Fiyat ve karat
Düşük kalitedeki elmasların fiyatları daha yüksektir, çünkü önemli bir şaşırtıcı değişken vardır: elmasın ağırlığı (carat). Elmasın ağırlığı, elmasın fiyatını belirlemek için en önemli tek faktördür ve düşük kaliteli elmaslar daha büyük olma eğilimindedir.
ggplot(diamonds, aes(carat, price)) +
geom_hex(bins = 50)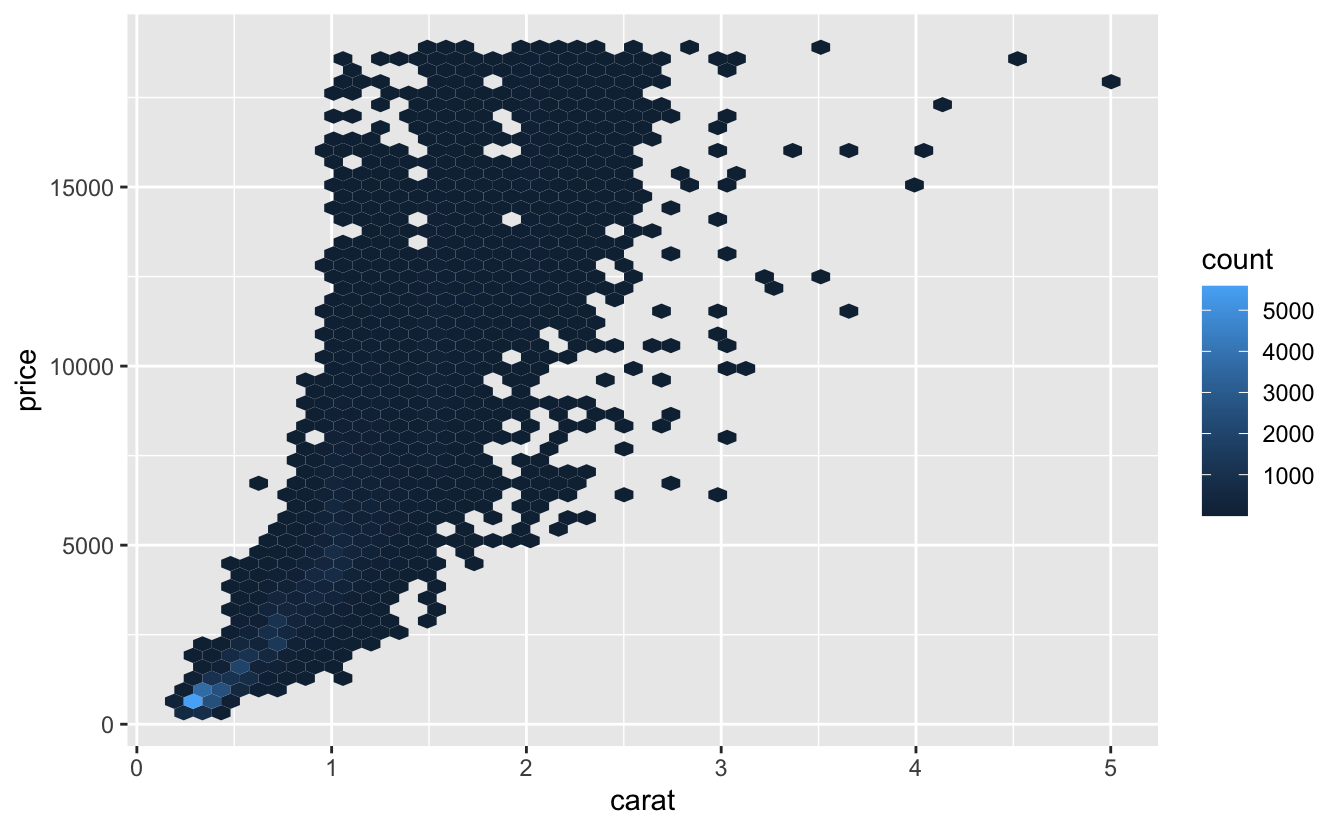
Bir elmasın carat etkisini ayrı turarak, diğer niteliklerinin nispi fiyatı nasıl etkilediğini bir model üzerine yerleştirerek görmeyi kolaylaştırabiliriz. Ama önce elmas veri setine bir kaç ince ayar yaparak çalışmayı daha kolay hale getirelim.
- 2,5 karattan küçük elmaslara odaklanın (verilerin %99.7’si).
- Karat ve fiyat değişkenlerine log-dönüşümü uygulayın.
diamonds2 <- diamonds %>%
filter(carat <= 2.5) %>%
mutate(lprice = log2(price), lcarat = log2(carat))Birlikte, bu değişiklikler carat ve price arasındaki ilişkiyi görmeyi kolaylaştırmaktadır:
ggplot(diamonds2, aes(lcarat, lprice)) +
geom_hex(bins = 50)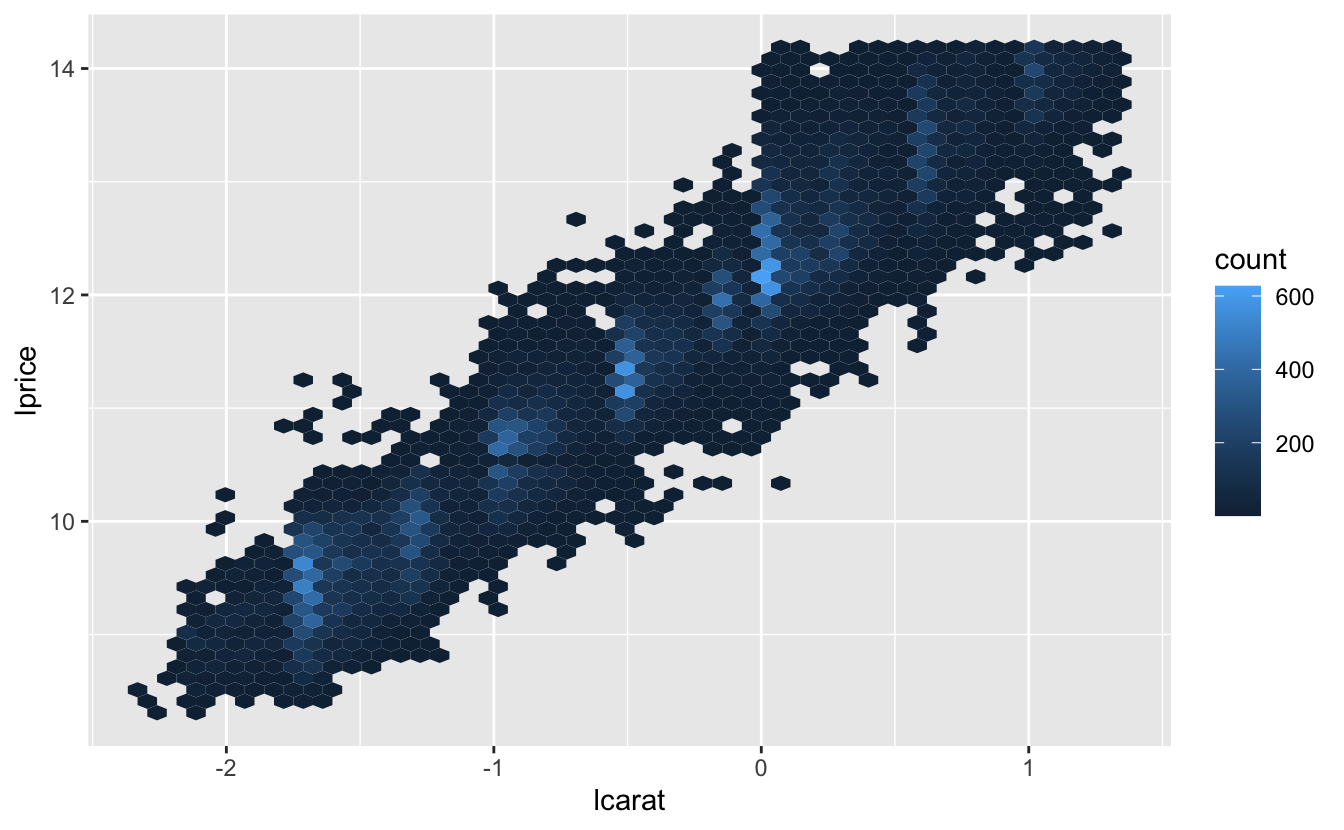
Log-dönüşümü burada özellikle kullanışlıdır, çünkü kalıbı doğrusal hale getirir ve doğrusal bir şekli çalışmak en kolay olanıdır. Bir sonraki adıma geçelim ve bu güçlü doğrusal kalıbı kaldıralım. Öncelikle bir model uygulayarak kalıbı belirgin hale getirelim:
mod_diamond <- lm(lprice ~ lcarat, data = diamonds2)Sonra modelin bize verilerle ilgili neler söylediğine bakalım. Log dönüşümü geri alarak, tahminleri geri dönüştürdüğüme dikkat edin, böylece ham verilerdeki tahminleri üst üste yerleştirebilirim:
grid <- diamonds2 %>%
data_grid(carat = seq_range(carat, 20)) %>%
mutate(lcarat = log2(carat)) %>%
add_predictions(mod_diamond, "lprice") %>%
mutate(price = 2 ^ lprice)
ggplot(diamonds2, aes(carat, price)) +
geom_hex(bins = 50) +
geom_line(data = grid, colour = "red", size = 1)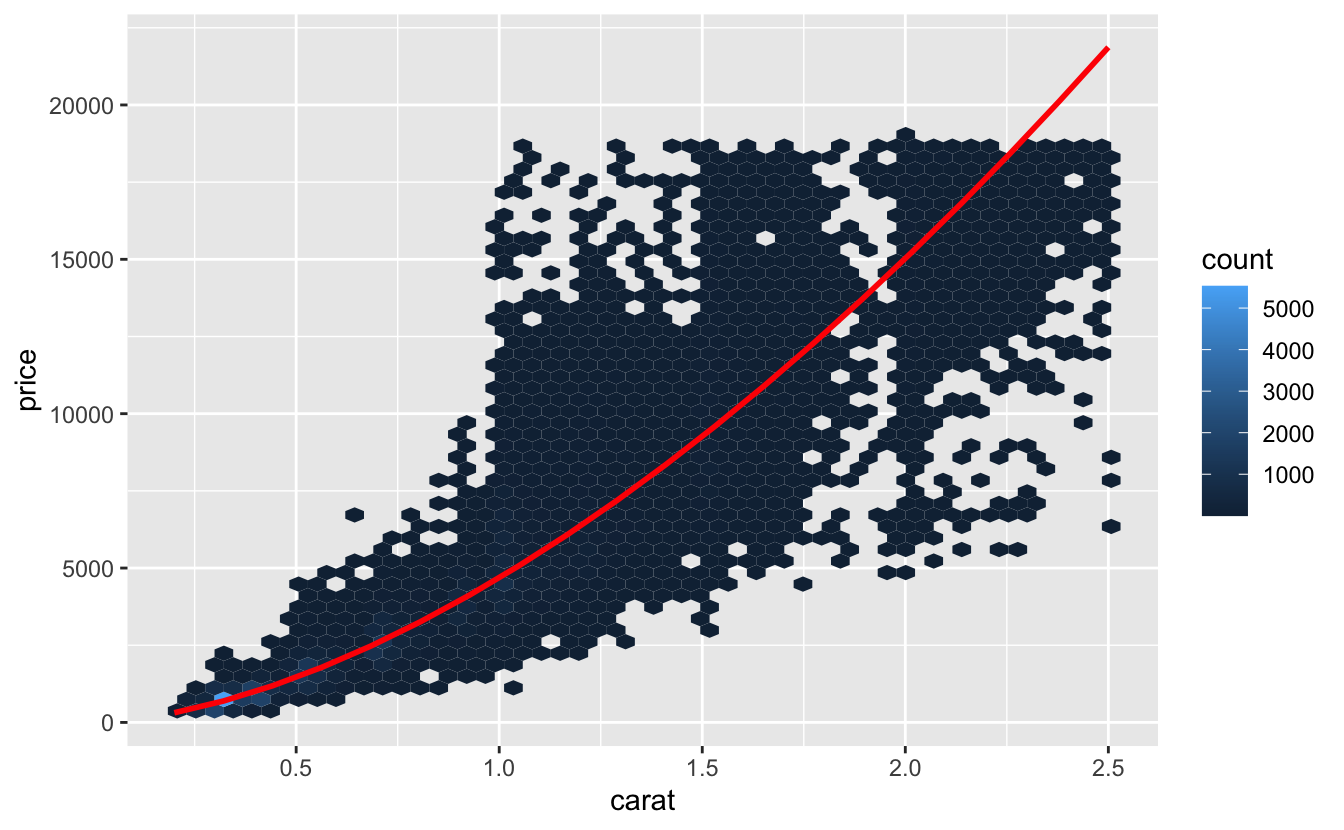
Bu bize verilerimizle ilgili ilginç bir şey anlatıyor. Eğer modelimize inanıyorsak, o halde büyük elmaslar beklenenden daha ucuzdur. Bunun sebebi muhtemelen bu veri setindeki hiç bir elmasın 19000$’dan daha yüksek bir fiyatta olmaması anlamına gelir.
Artık, güçlü doğrusal deseni başarıyla ortadan kaldırdığımızı doğrulayan artıklara bakabiliriz:
diamonds2 <- diamonds2 %>%
add_residuals(mod_diamond, "lresid")
ggplot(diamonds2, aes(lcarat, lresid)) +
geom_hex(bins = 50)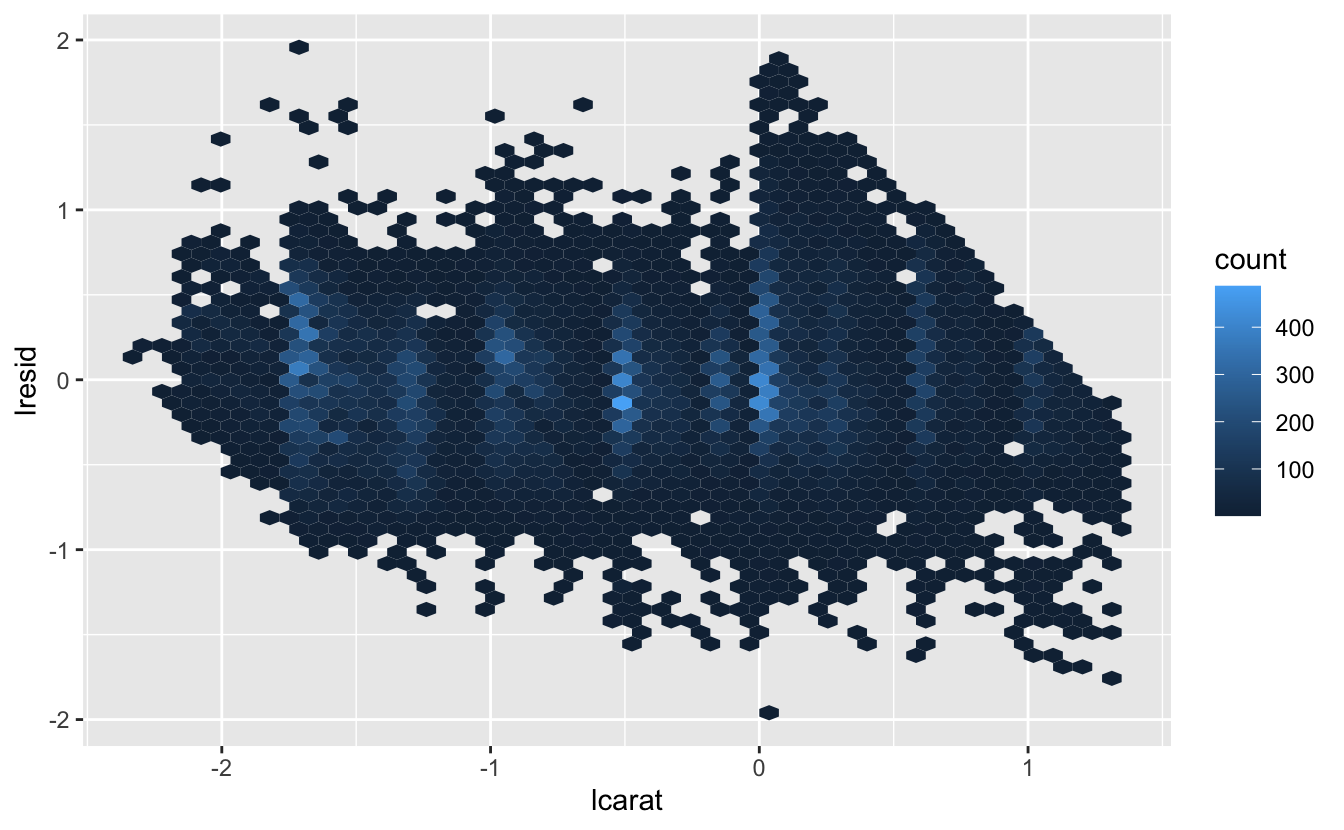
En önemlisi, artık price yerine bu artıkları kullanarak bizi motive eden grafiklerimizi tekrar yapabiliriz.
ggplot(diamonds2, aes(cut, lresid)) + geom_boxplot()
ggplot(diamonds2, aes(color, lresid)) + geom_boxplot()
ggplot(diamonds2, aes(clarity, lresid)) + geom_boxplot()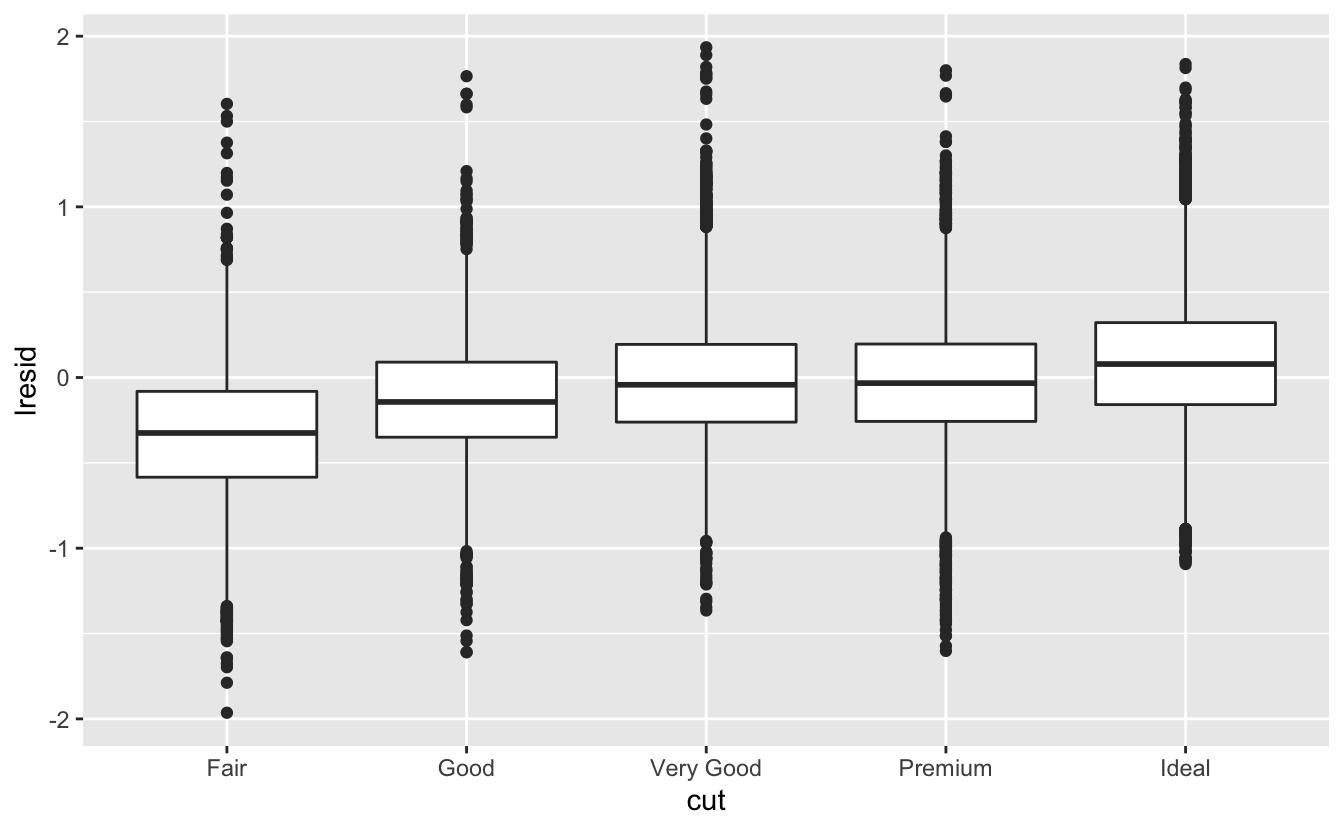
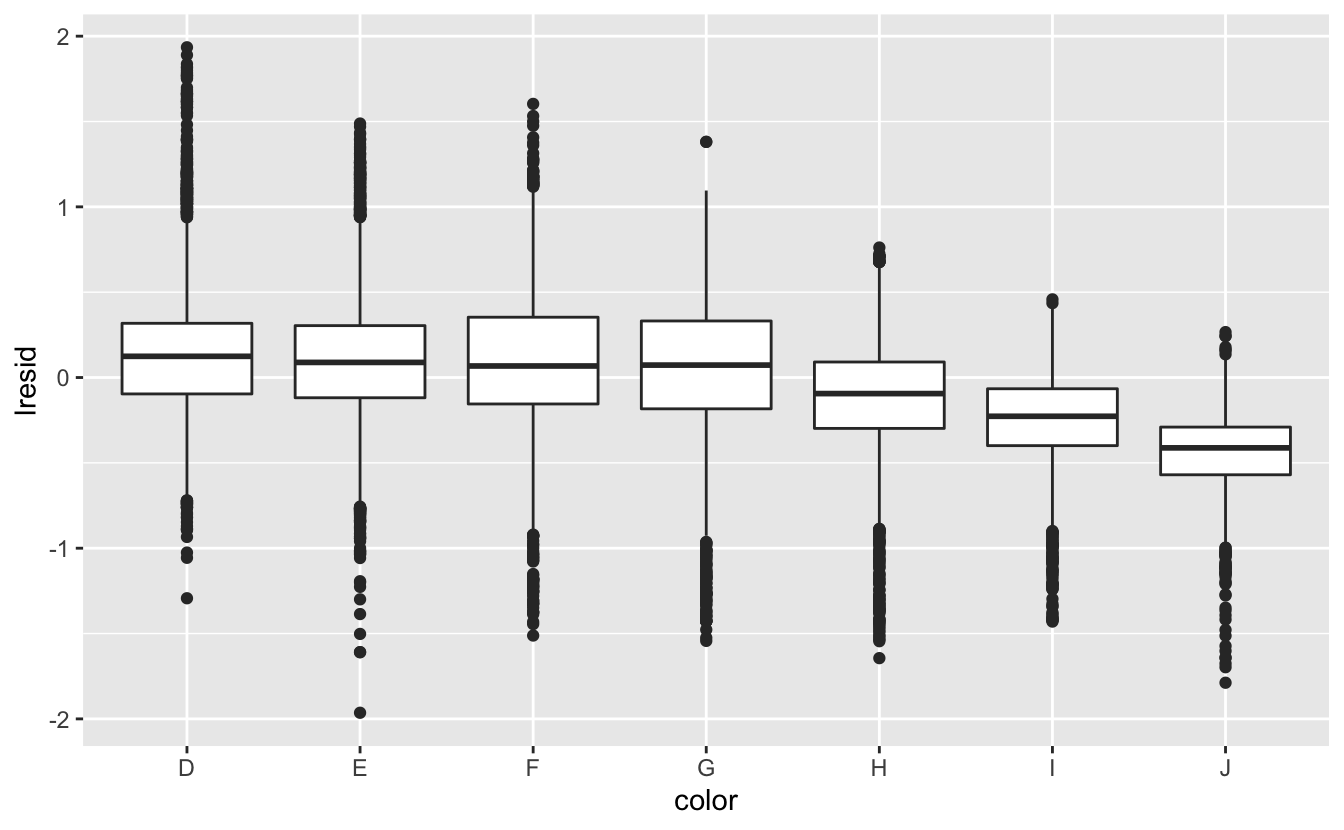
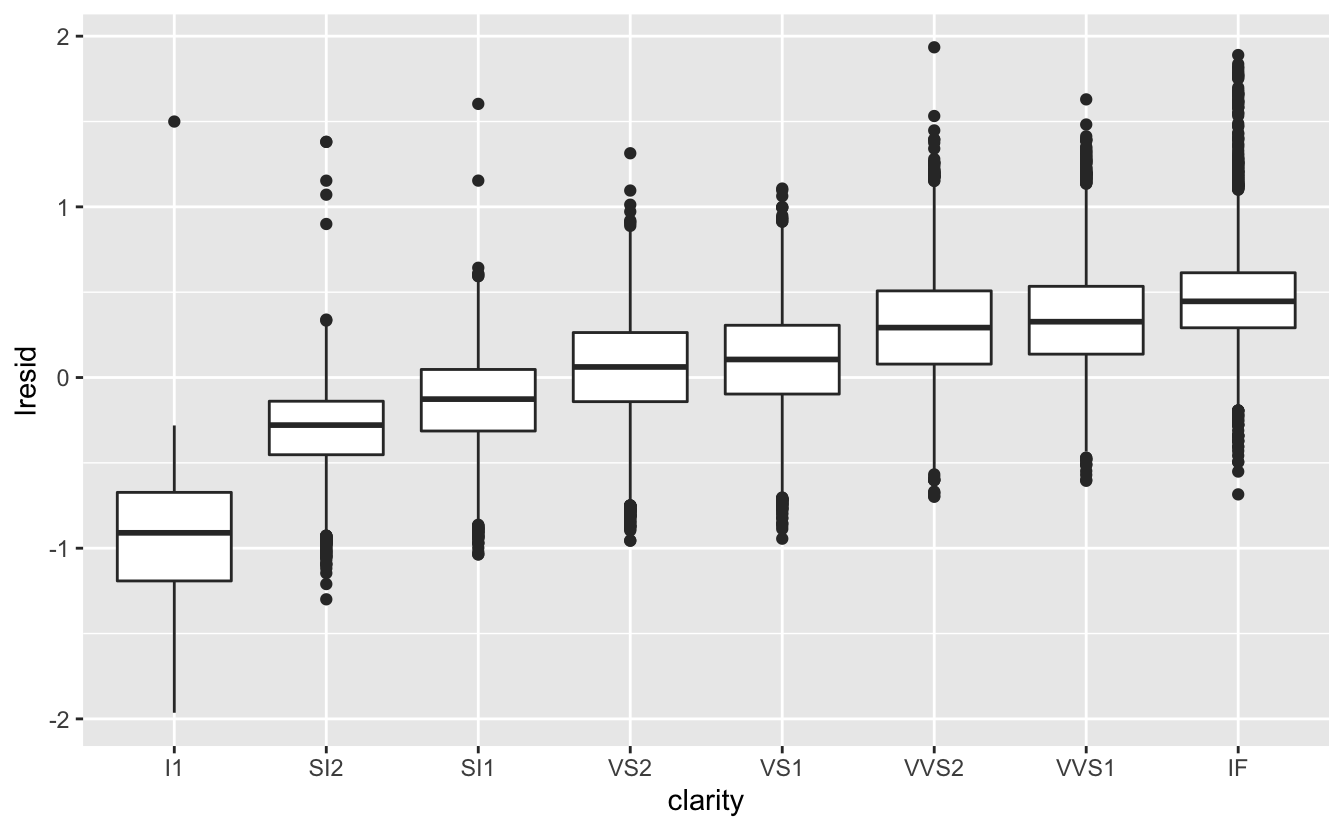
Artık beklediğimiz ilişkiyi görüyoruz: elmasın kalitesi arttıkça, buna göre fiyatı da artmaktadır. Y eksenini yorumlamak için, artıkların bize ne söylediğini ve hangi ölçekte oldukları üzerine düşünmemiz gerekir. Artığın -1 olması lprice’ın sadece ağırlığına dayanan bir tahminden 1 birim daha düşük olduğunu gösterir. \(2^{-1}\), 1/2’dir. Dolayısıyla, -1 değerinde olan noktalar beklenen fiyatın yarısı iken, 1 değeri olan artıklar öngörülen fiyatın iki katıdır.
24.2.2 Daha karmaşık bir model
Eğer istersek, modelimizi geliştirmeye devam edebilir, model içerisinde gözlemlediğimiz etkileri ortadan kaldırarak, onları daha görünür hale getirebiliriz. Örneğin, color, cut ve clarity kriterlerini model içerisine dahil ederek, böylelikle bu üç kategorik değişkenlşerin etkilerini ortaya çıkartabiliriz.
mod_diamond2 <- lm(lprice ~ lcarat + color + cut + clarity, data = diamonds2)Bu model şu anda dört tahmin edici içermektedir, bu sebeple görselleştirmesi zorlaşmaktadır. Neyse ki, hali hazırda şu an hepsi birbirinden bağımsız durumdalar, bu da onları ayrı ayrı dört alana yerleştirebileceğimiz anlamına gelir.
grid <- diamonds2 %>%
data_grid(cut, .model = mod_diamond2) %>%
add_predictions(mod_diamond2)
grid
#> # A tibble: 5 × 5
#> cut lcarat color clarity pred
#> <ord> <dbl> <chr> <chr> <dbl>
#> 1 Fair -0.515 G VS2 11.2
#> 2 Good -0.515 G VS2 11.3
#> 3 Very Good -0.515 G VS2 11.4
#> 4 Premium -0.515 G VS2 11.4
#> 5 Ideal -0.515 G VS2 11.4
ggplot(grid, aes(cut, pred)) +
geom_point()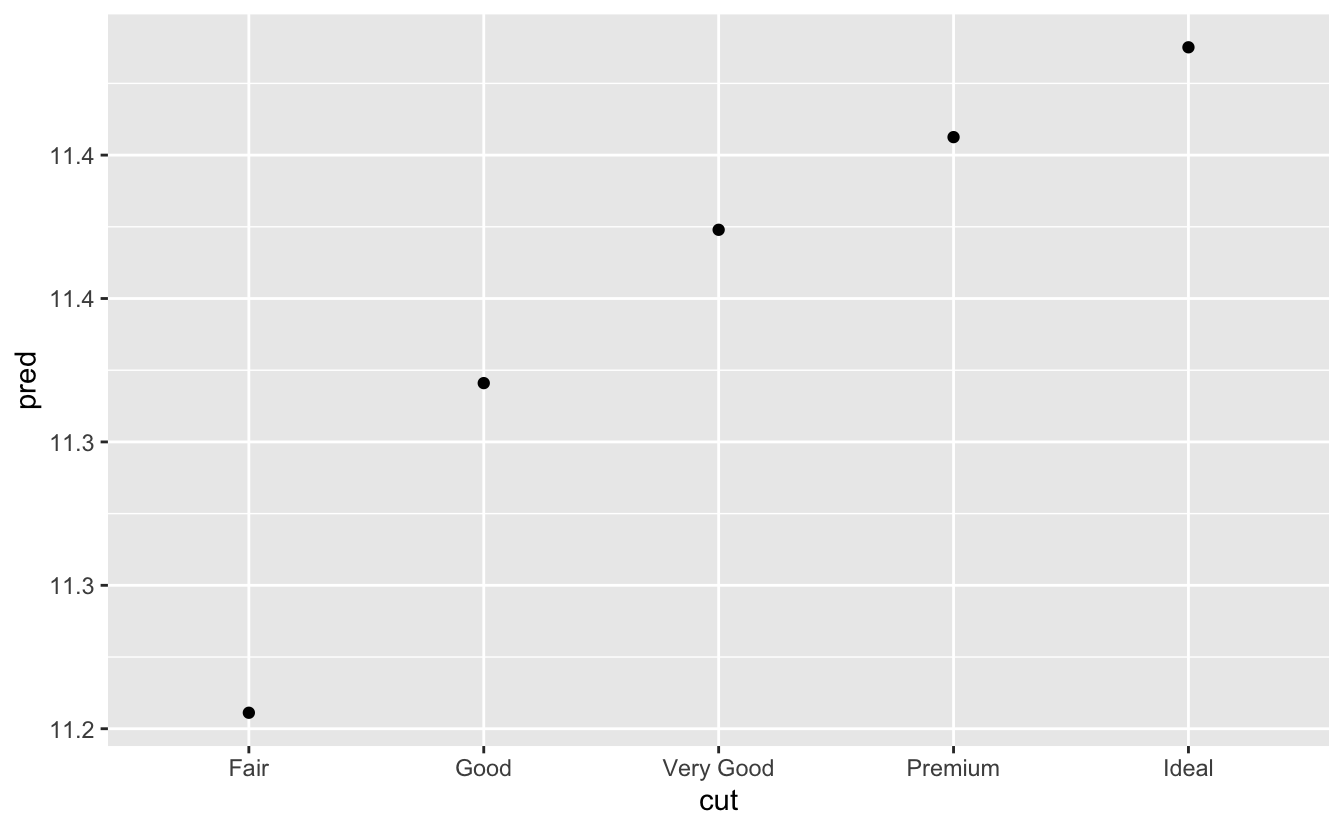
Model, açıkça sağlamadığınız değişkenlere ihtiyaç duyuyorsa, data_grid() bunları otomatik olarak “tipik” değerlerle doldurur. Sürekli değişkenler için ortanca değer ve kategorik değişkenler için ise en yaygın değeri kullanır (veya bir bağlantı varsa değerleri).
diamonds2 <- diamonds2 %>%
add_residuals(mod_diamond2, "lresid2")
ggplot(diamonds2, aes(lcarat, lresid2)) +
geom_hex(bins = 50)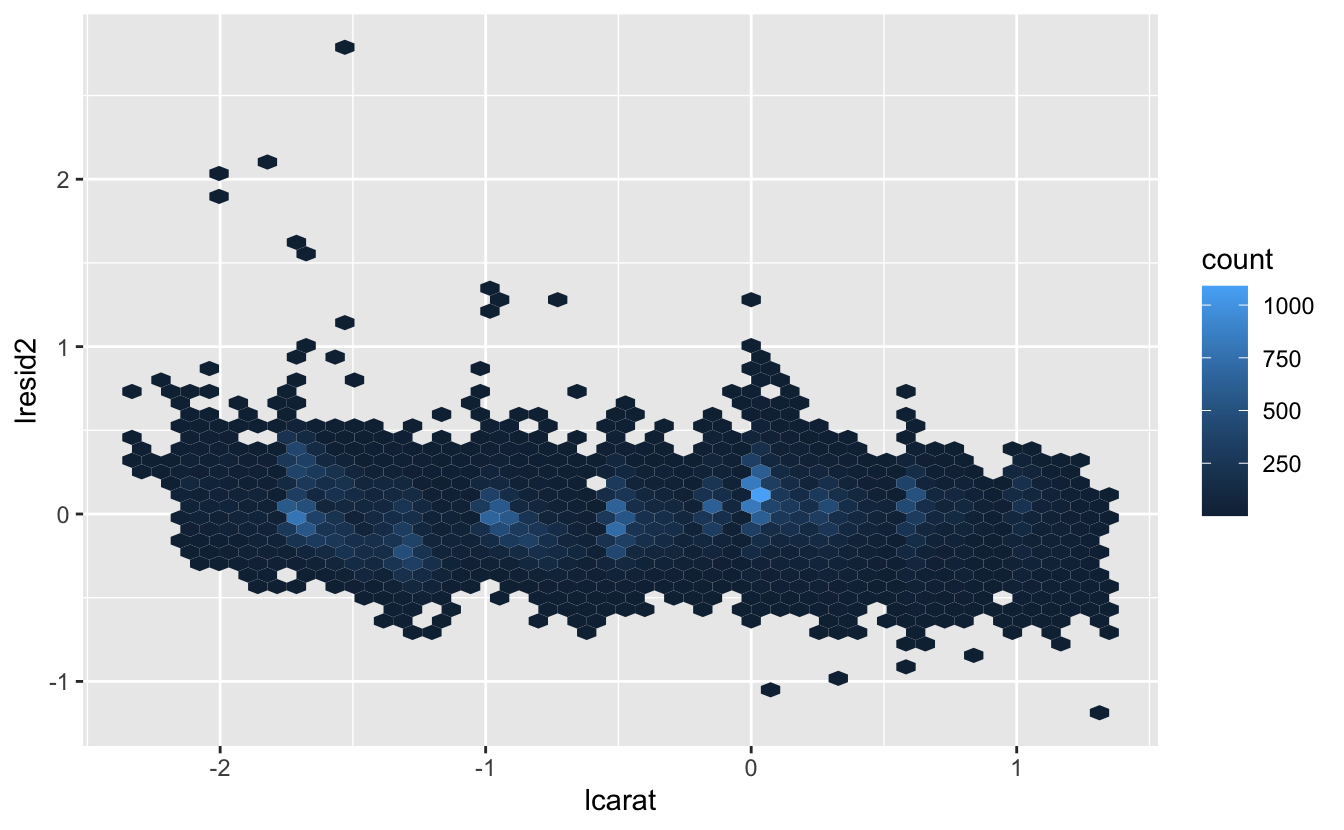
Bu grafik oldukça büyük artıkları olan bazı elmasların var olduğunu göstermektedir - hatırlayın 2’lik bir artık, elmasın beklediğimiz fiyatının 4 katı olduğunu göstermektedir.
diamonds2 %>%
filter(abs(lresid2) > 1) %>%
add_predictions(mod_diamond2) %>%
mutate(pred = round(2 ^ pred)) %>%
select(price, pred, carat:table, x:z) %>%
arrange(price)
#> # A tibble: 16 × 11
#> price pred carat cut color clarity depth table x y z
#> <int> <dbl> <dbl> <ord> <ord> <ord> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 1013 264 0.25 Fair F SI2 54.4 64 4.3 4.23 2.32
#> 2 1186 284 0.25 Premium G SI2 59 60 5.33 5.28 3.12
#> 3 1186 284 0.25 Premium G SI2 58.8 60 5.33 5.28 3.12
#> 4 1262 2644 1.03 Fair E I1 78.2 54 5.72 5.59 4.42
#> 5 1415 639 0.35 Fair G VS2 65.9 54 5.57 5.53 3.66
#> 6 1415 639 0.35 Fair G VS2 65.9 54 5.57 5.53 3.66
#> # … with 10 more rowsBu noktada gerçekten bana hiçbir şey ifade etmiyor, ancak bunun modelimizle ilgili bir sorun olup olmadığını veya verilerde hata olup olmadığını düşünerek zaman harcamakta fayda var. Verilerde hatalar varsa, yanlış fiyatlandırılmış elmasları satın almak için bir fırsat olabilir.
24.2.3 Uygulamalar
lcaratvs.lpricegrafiğinde açık renkli bazı dikey çizgiler mevcut. Neyi temsil etmektedirler?Eğer
log(price) = a_0 + a_1 * log(carat)ise,
pricevecaratarasındaki ilişki hakkında ne söylüyor demektir?Çok yüksek ve çok düşük artıklara sahip olan elmasları çıkartın. Bu elmaslarla ilgili olağandışı bir şey var mı? Özellikle kötü mü veya iyi mi, yoksa fiyatlandırmada hata olduğunu mu düşünüyorsunuz?
Son model
mod_diamond2, elmas fiyatlarının tahmininde iyi bir iş çıkardı mı? Elmas satın alıyor olsaydınız, ne kadar harcamanız gerektiğini söylediğinde güvenir miydiniz?
24.3 Günlük uçuş sayılarını ne etkiler?
İlk bakışta bir veri seti için nispeten daha kolay görünen, benzer bir işlemle çalışmaya başlayalım: New York şehrinden (NYC) kalkan uçuşların günlük sayısı. Bu gerçekten küçük bir veri setidir — sadece 365 satır ve 2 sütun — her şeyi ortaya çıkaran bir model ile sonlandırmayacağız ancak göreceğiniz üzere süreçte izleyeceğimiz adımlar bize veriyi daha iyi anlamamızı sağlayacak. Günlük uçuş sayısı sayarak ve ggplot2 ile görselleştirerek başlayalım.
daily <- flights %>%
mutate(date = make_date(year, month, day)) %>%
group_by(date) %>%
summarise(n = n())
daily
#> # A tibble: 365 × 2
#> date n
#> <date> <int>
#> 1 2013-01-01 842
#> 2 2013-01-02 943
#> 3 2013-01-03 914
#> 4 2013-01-04 915
#> 5 2013-01-05 720
#> 6 2013-01-06 832
#> # … with 359 more rows
ggplot(daily, aes(date, n)) +
geom_line()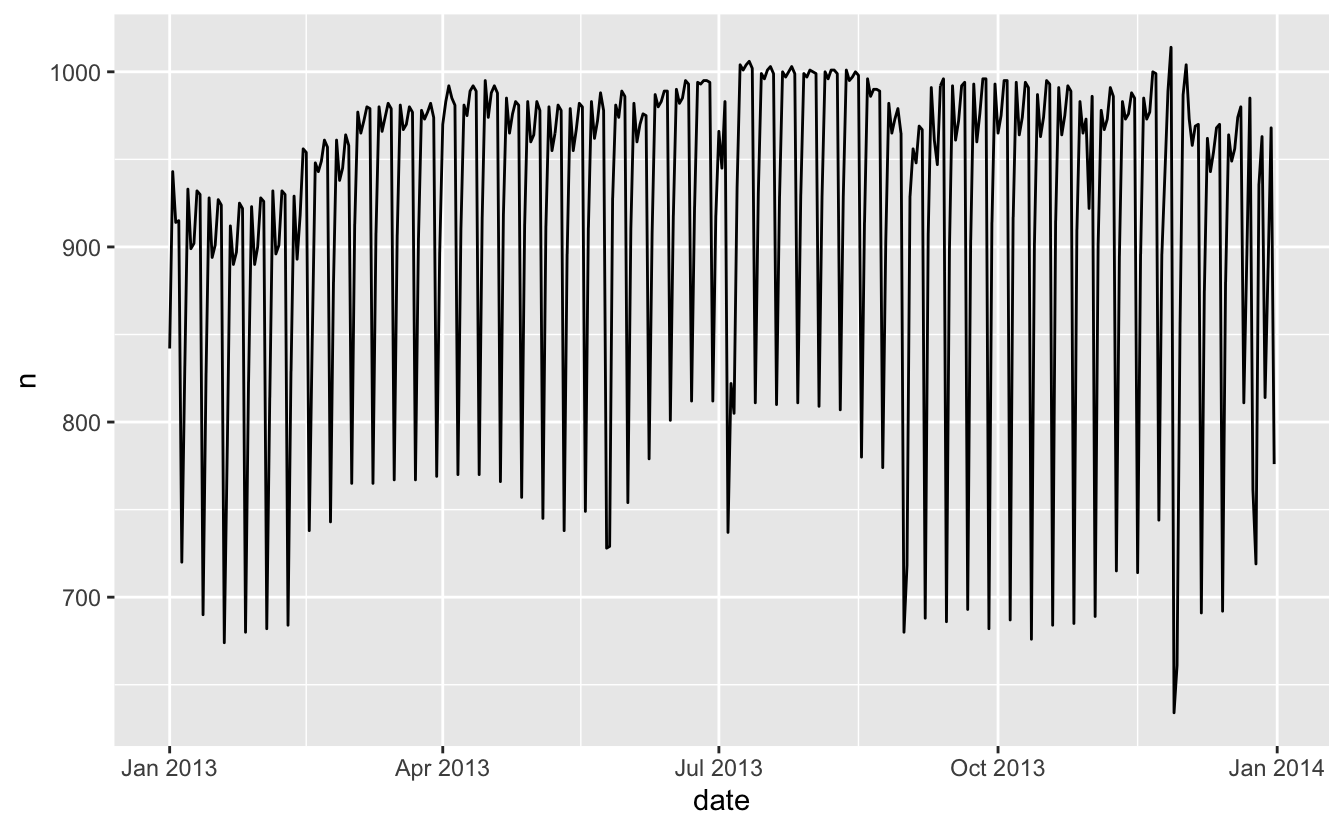
24.3.1 Haftanın günü
Uzun vadeli eğilimi anlamak güçtür, çünkü hassas ayrıntıları baskılayan haftanın en yoğun günü etkisi vardır. Uçuş numaralarının haftanın gününe göre dağılımına bakarak başlayalım:
daily <- daily %>%
mutate(wday = wday(date, label = TRUE))
ggplot(daily, aes(wday, n)) +
geom_boxplot()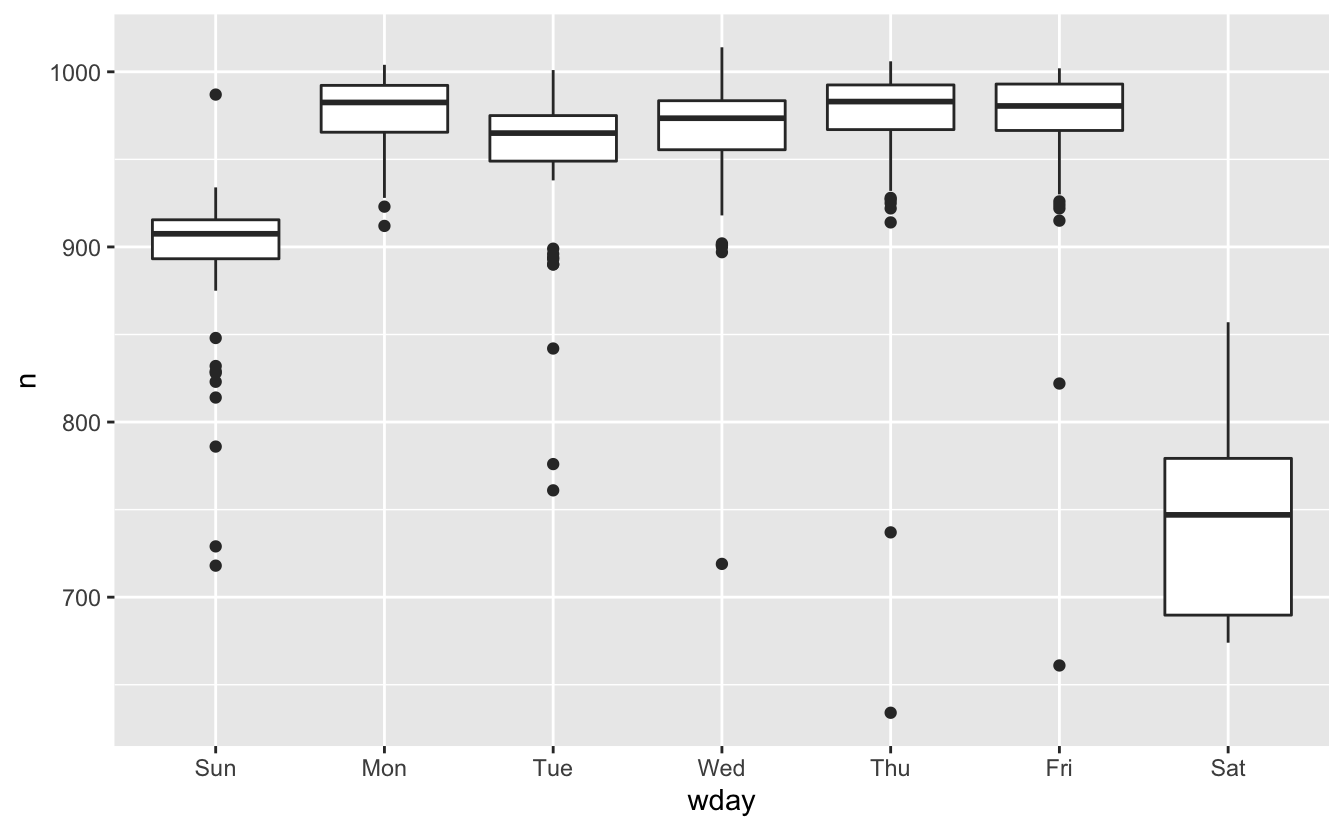
Çoğu seyahat iş için olduğundan, hafta sonları daha az uçuş vardır. Etkisi özellikle Cumartesi günleri ortaya çıkmaktadır: Bazen Pazartesi sabahı toplantısı için Pazar gününden ayrılmanız gerekebilir, ancak aileniz ile evde vakit geçirebilecekken Cumartesi günü ayrılmak çok nadirdir.
Bu ilişkiyi kaldırmanın bir yolu da bir model kullanmaktır. İlk olarak, modeli yerleştiririz ve orjinal veriler üzerine tahminleri bindirerek gösteririz:
mod <- lm(n ~ wday, data = daily)
grid <- daily %>%
data_grid(wday) %>%
add_predictions(mod, "n")
ggplot(daily, aes(wday, n)) +
geom_boxplot() +
geom_point(data = grid, colour = "red", size = 4)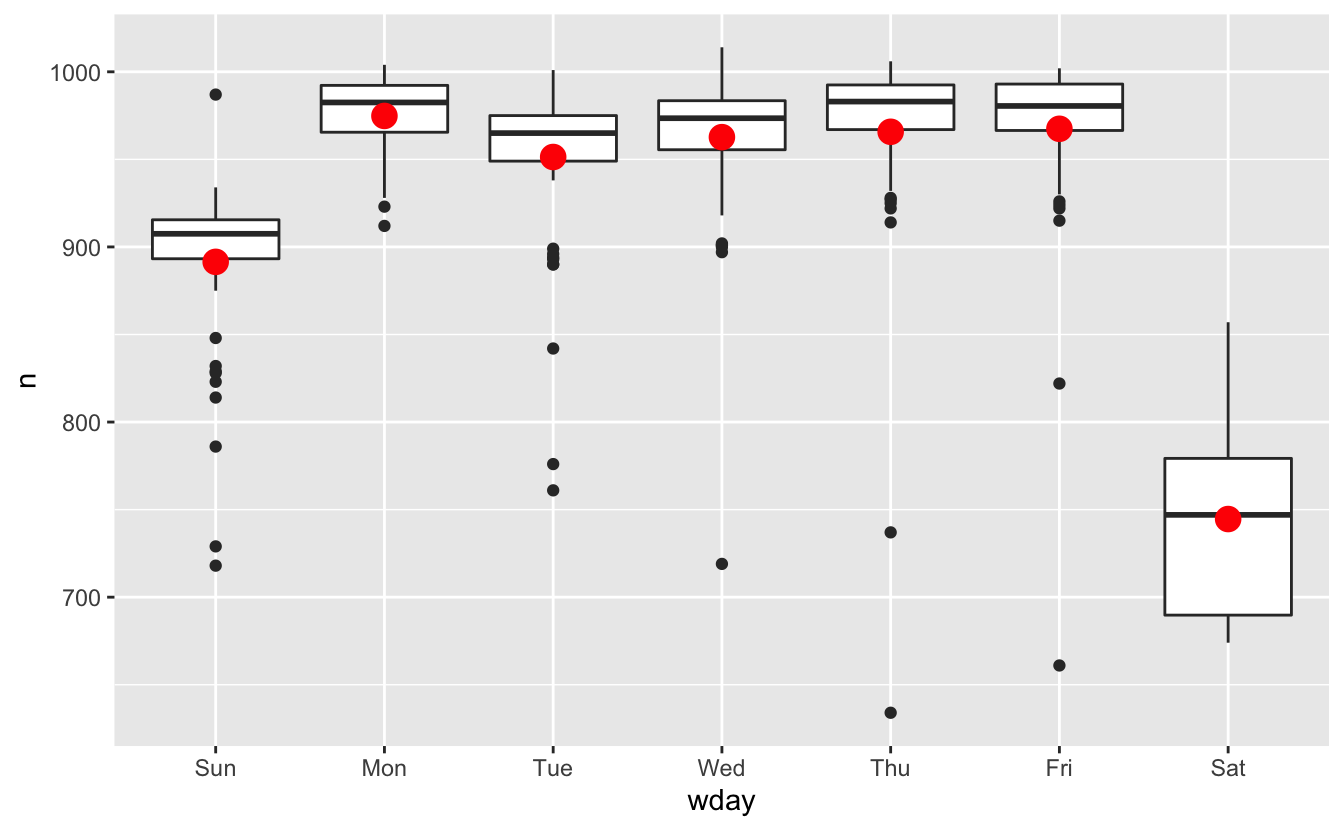
Devamında, hesaplama yapıyor ve artıkları görselleştiriyoruz.
daily <- daily %>%
add_residuals(mod)
daily %>%
ggplot(aes(date, resid)) +
geom_ref_line(h = 0) +
geom_line()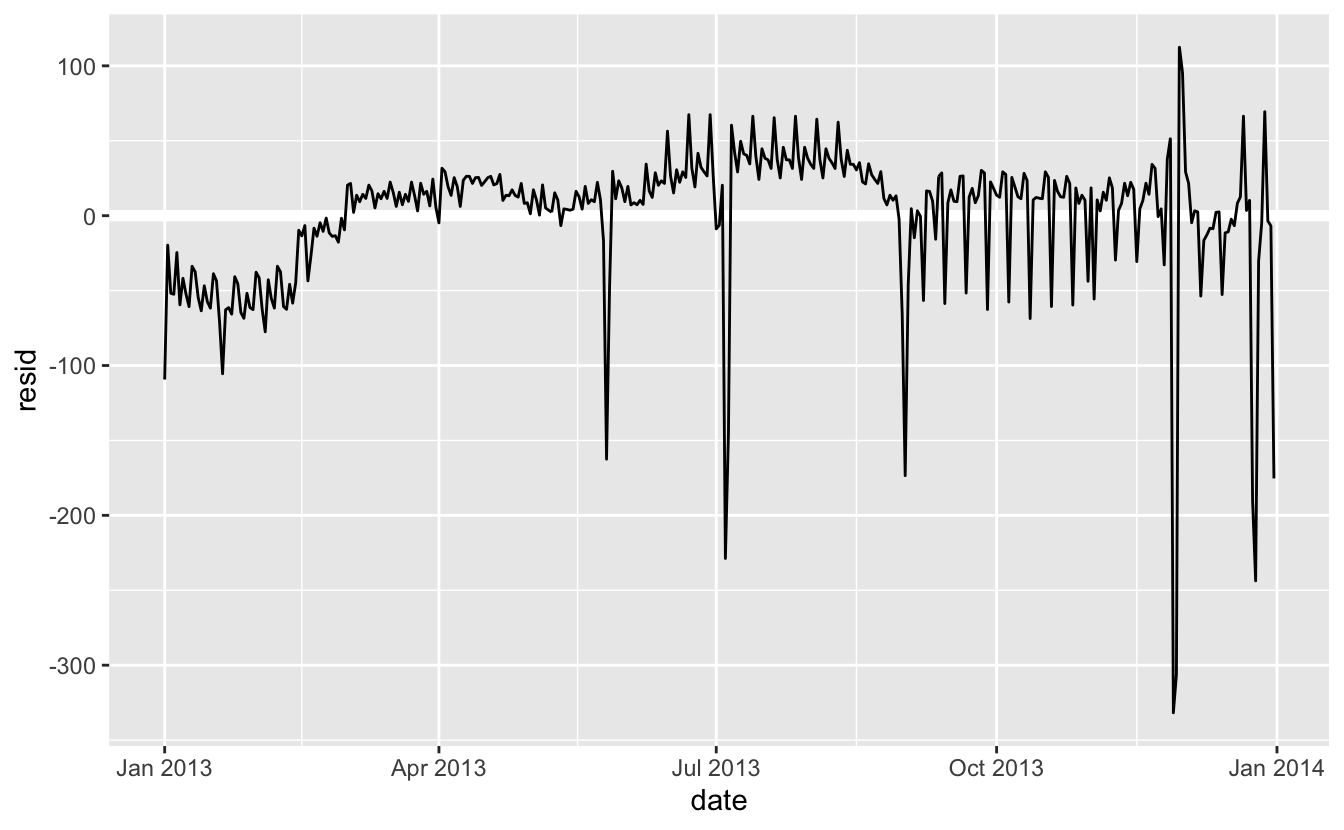
Y eksenindeki değişime dikkat edin: artık haftanın gününe göre beklenen uçuş sayısından sapmayı görüyoruz. Bu grafik kullanışlıdır, çünkü haftanın büyük gününe ait etkinin çoğunu kaldırdığımızdan, kalan daha hassas dağılımların bazılarını görebiliriz:
- Modelimiz Haziran ayından itibaren başarısız gözüküyor: Hala modelimizin yakalayamadığı güçlü ve düzenli şekli görebilirsiniz. Haftanın her bir günü için bir plot ile beraber bir hat çizdirmek sebebi görmemizi kolaylaştırır:
ggplot(daily, aes(date, resid, colour = wday)) +
geom_ref_line(h = 0) +
geom_line()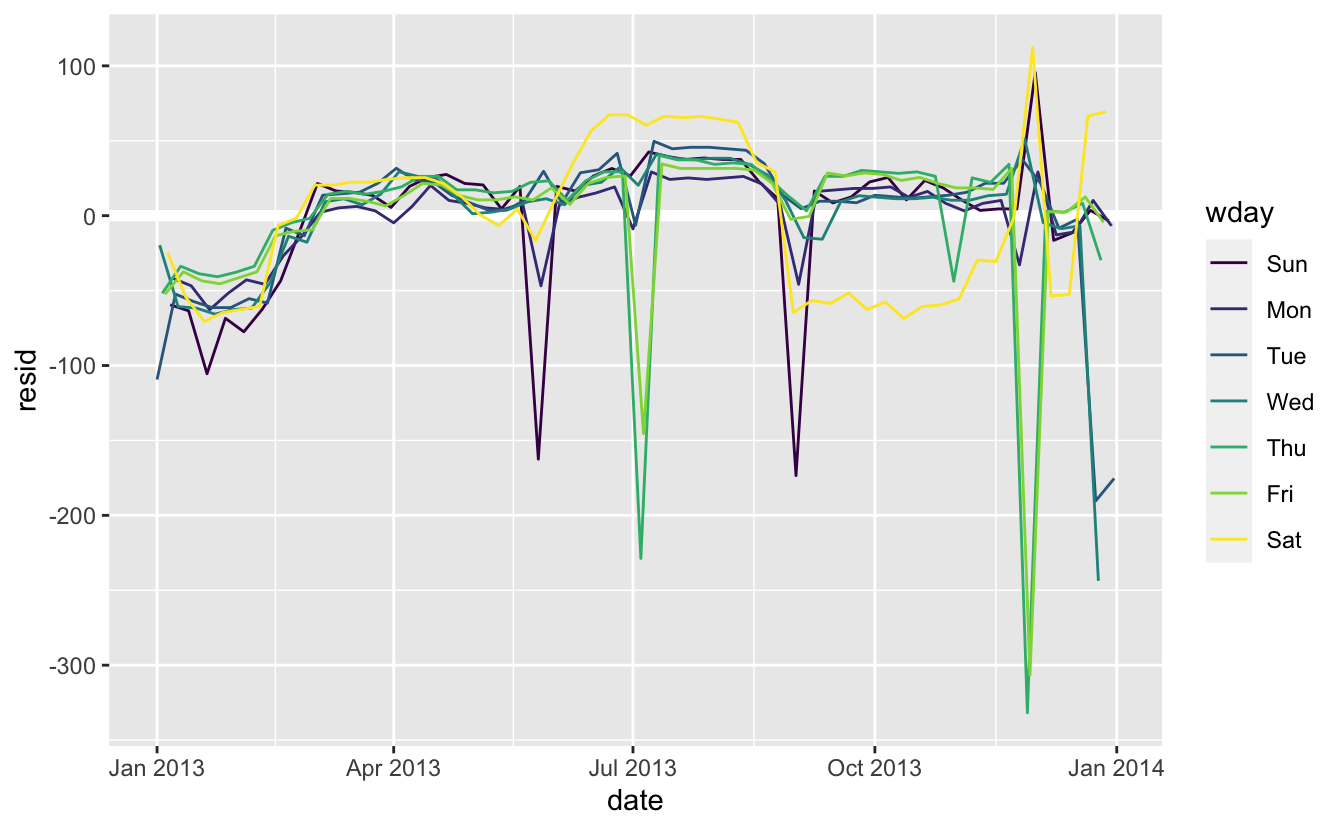
Modelimiz Cumartesi günü yapılan uçuşların sayısını doğru olarak tahmin edememektedir: Yaz aylarında beklediğimizden daha fazla uçuş varken, Güz döneminde daha azdır. Bir sonraki bölümde bu düzeni yakalamak için daha iyi nasıl yapabileceğimizi göreceğiz.
- Beklenenden çok daha az sayıda uçuş olan birkaç gün var:
daily %>%
filter(resid < -100)
#> # A tibble: 11 × 4
#> date n wday resid
#> <date> <int> <ord> <dbl>
#> 1 2013-01-01 842 Tue -109.
#> 2 2013-01-20 786 Sun -105.
#> 3 2013-05-26 729 Sun -162.
#> 4 2013-07-04 737 Thu -229.
#> 5 2013-07-05 822 Fri -145.
#> 6 2013-09-01 718 Sun -173.
#> # … with 5 more rowsAmerikalıların resmi tatillerine aşina iseniz, 4 Temmuz, Şükran Günü, Noel ve Yeni Yıl’ı görebilirsiniz. Elbette resmi tatillere örtüşmeyen bazı durumlar da mevcuttur. Alıştırmaların birinde bunlar üzerine çalışacaksınız.
- Tüm bir yıl boyunca biraz daha uzun vadeli bir eğilim var gibi görünmektedir. Bu eğilimi
geom_smooth()ile vurgulayabiliriz.
daily %>%
ggplot(aes(date, resid)) +
geom_ref_line(h = 0) +
geom_line(colour = "grey50") +
geom_smooth(se = FALSE, span = 0.20)
#> `geom_smooth()` using method = 'loess' and formula 'y ~ x'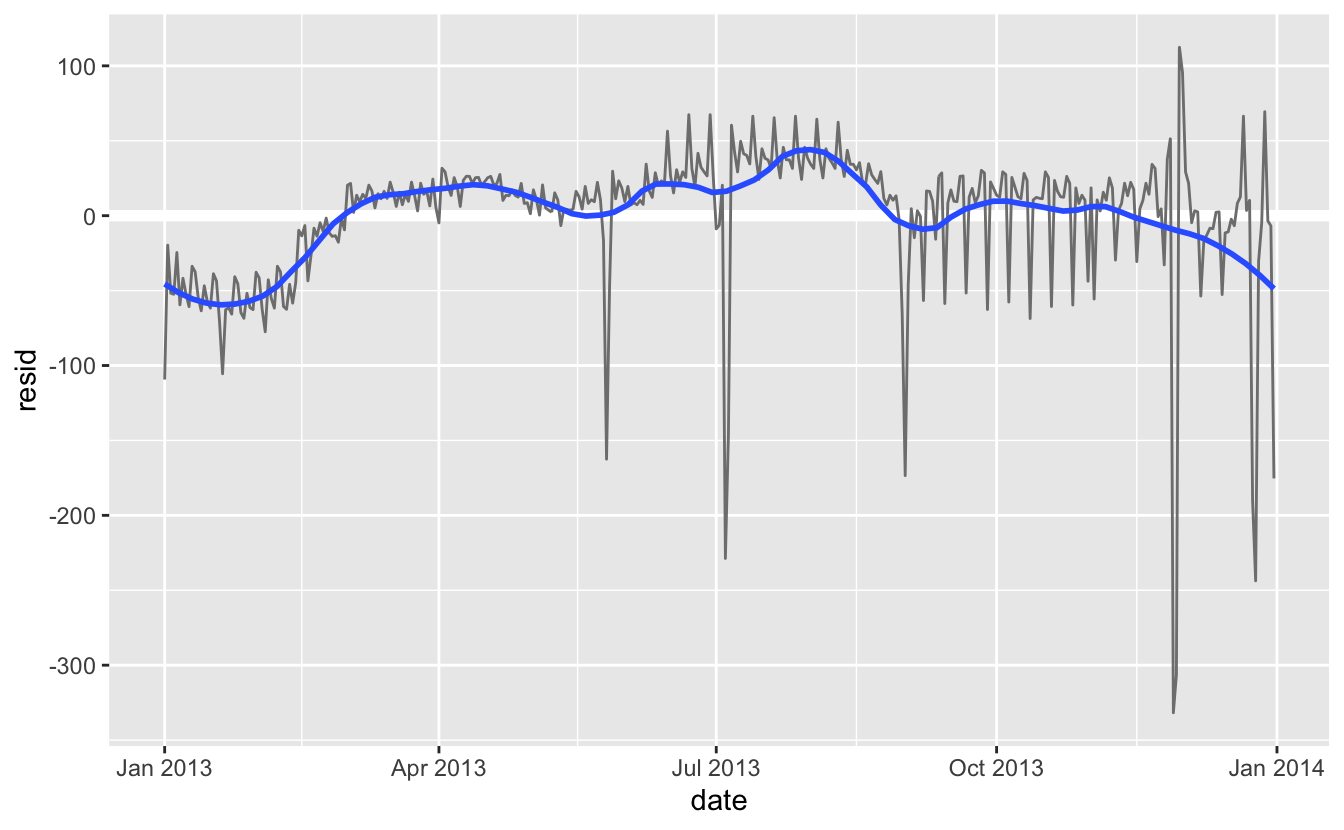
Ocak (ve Aralık) aylarında daha az iken, yazları (Mayıs-Eylül) daha fazla uçuş yapılmaktadır. Bu örnekle nicel olarak fazla bir şey yapamayız, çünkü sadece bir yıllık veriye sahibiz. Fakat potansiyel açıklamalar üzerine beyin fırtınası yapmak adına alan bilgilerimizi kullanabiliriz.
24.3.2 Mevsimsel cumartesi etkisi
Öncelikle Cumartesi günü yapılan uçuş sayısını doğru tahmin edemememizle başa çıkalım. Başlamak için iyi bir nokta, Cumartesi günlerine odaklanarak ham sayılara geri dönmektir:
daily %>%
filter(wday == "Cts") %>%
ggplot(aes(date, n)) +
geom_point() +
geom_line() +
scale_x_date(NULL, date_breaks = "1 month", date_labels = "%b")
(Verileri ve enterpolasyonun ne olduğunu daha net göstermek için hem noktaları hem de çizgileri kullandım.)
Bu dağılımın yaz tatillerinden kaynaklandığına şüpheleniyorum: çoğu insan yaz aylarında tatile gidiyor ve insanlar Cumartesi günleri tatil için seyahat etmeyi umursamıyorlar. Bu grafiğe bakacak olursak, yaz tatillerinin Haziran ayının başından Ağustos ayının sonlarına kadar olduğunu tahmin edebiliriz. Bu, devletin okul programına oldukça uyuyor: 2013 yılında yaz tatili 26 Haziran - 9 Eylül tarihleri arasındaydı.
İlkbahardaki Cumartesi uçuşları neden Sonbahardan daha fazladır? Bazı Amerikalı arkadaşlarıma sordum ve onlar uzun süren Şükran Günü ve Noel tatili nedeniyle Güz döneminde aile tatillerini planlamanın daha az yaygın olduğunu belirttiler. Kesin olarak kabul edecek verimiz yok, ancak makul bir çalışma hipotezi gibi görülüyor.
Okul ile ilgili üç durumu kapsayan bir “dönem (term)” değişkeni oluşturalım ve çalışmamızı bir grafik ile kontrol edelim.
term <- function(date) {
cut(date,
breaks = ymd(20130101, 20130605, 20130825, 20140101),
labels = c("bahar", "yaz", "sonbahar")
)
}
daily <- daily %>%
mutate(term = term(date))
daily %>%
filter(wday == "Cts") %>%
ggplot(aes(date, n, colour = term)) +
geom_point(alpha = 1/3) +
geom_line() +
scale_x_date(NULL, date_breaks = "1 month", date_labels = "%b")
(Grafikte güzel aralıklar elde edebilmek için tarihleri manuel olarak ayarladım. Fonksiyonunuzun ne yapıtığını anlamanıza yardımcı olacak bir görselleştirme kullanmak, oldukça güçlü ve genel bir tekniktir.)
Bu yeni değişkenin haftanın diğer günlerini nasıl etkilediğini görmek faydalı olacaktır:
daily %>%
ggplot(aes(wday, n, colour = term)) +
geom_boxplot()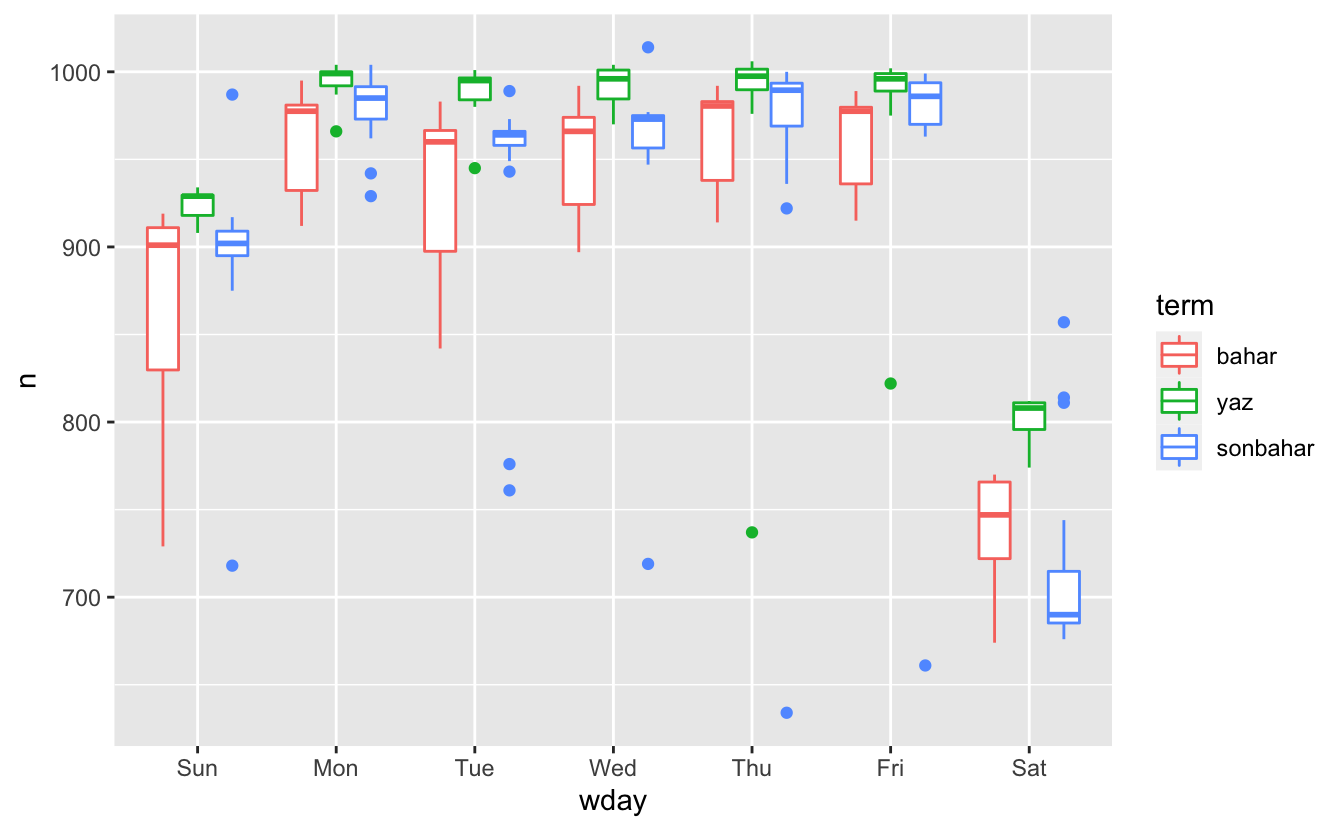
Dönemler arasında önemli farklılıklar var gibi gözüküyor, bu nedenle her dönemi haftanın ayrı bir gününe yerleştirmek makuldur. Bu, modelimizi geliştirir, ancak umduğumuz kadar değil:
mod1 <- lm(n ~ wday, data = daily)
mod2 <- lm(n ~ wday * term, data = daily)
daily %>%
gather_residuals(without_term = mod1, with_term = mod2) %>%
ggplot(aes(date, resid, colour = model)) +
geom_line(alpha = 0.75)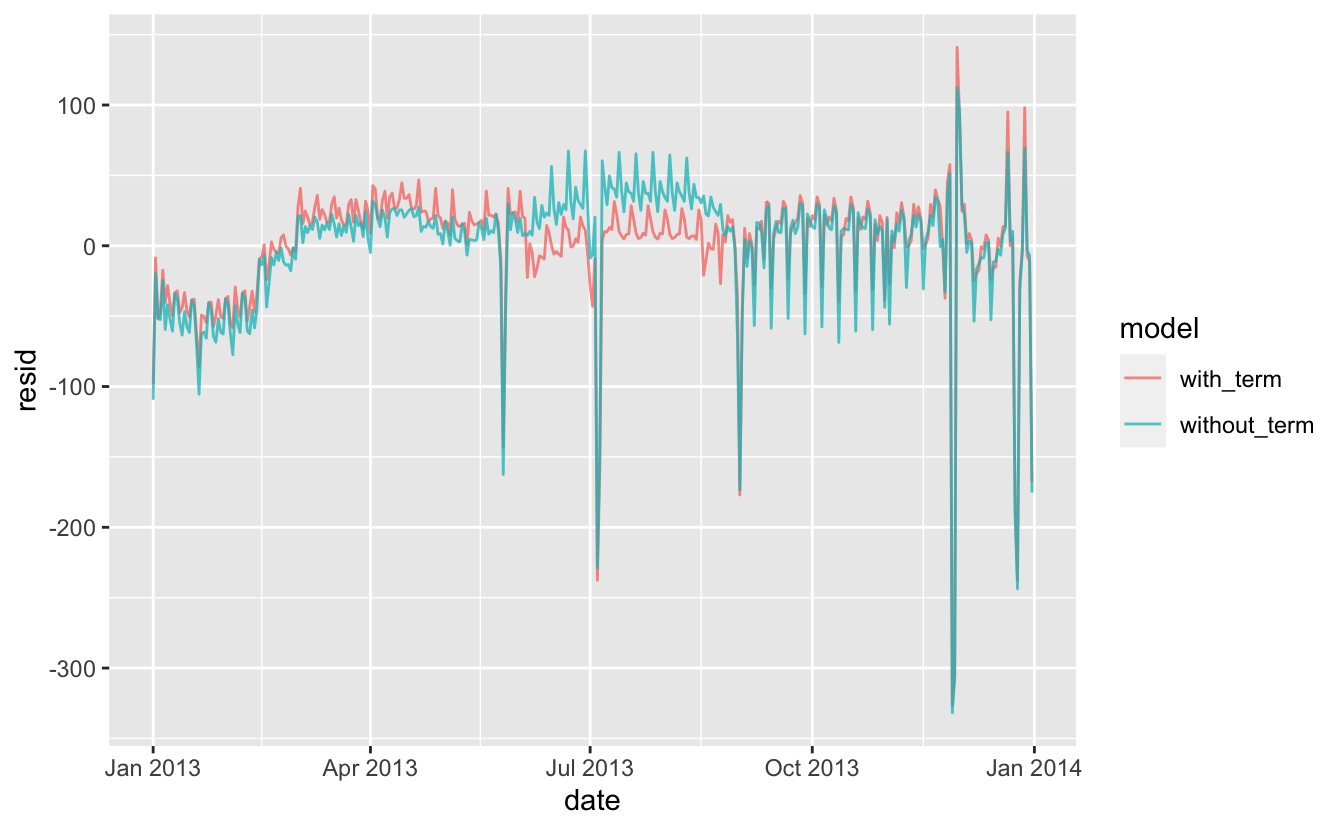
Modelimizden ham verilere ilişkin öngörüleri, üst üste bindirerek sorunu görebiliriz:
grid <- daily %>%
data_grid(wday, term) %>%
add_predictions(mod2, "n")
ggplot(daily, aes(wday, n)) +
geom_boxplot() +
geom_point(data = grid, colour = "red") +
facet_wrap(~ term)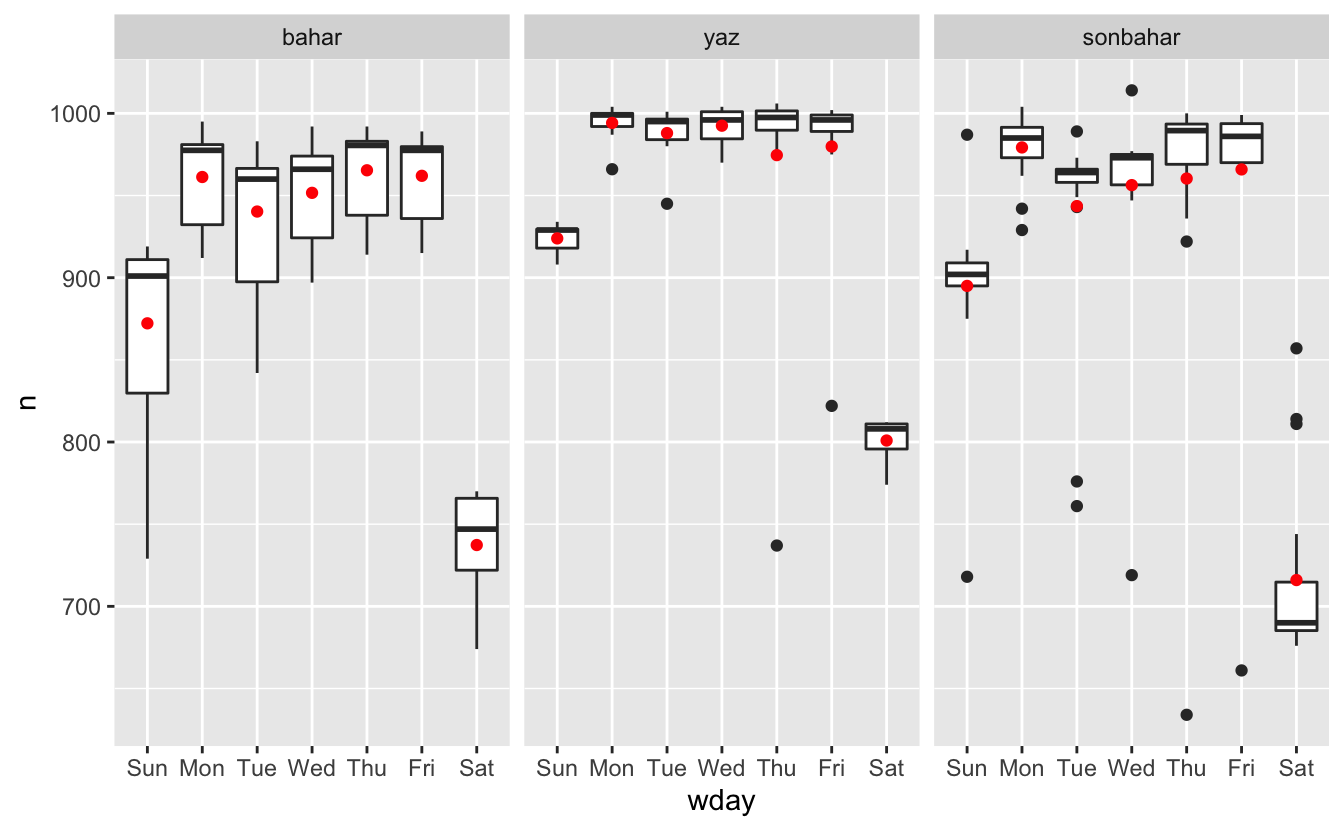
Modelimiz ortalama etkiyi bulmakta, ancak çok fazla aykırı değere sahibiz, bu nedenle ortalama tipik değerden çok uzak olma eğilimindedir. Aykırı değerlerin etkisine karşılık dayanıklı bir model kullanarak bu sorunu hafifletebiliriz: MASS::rlm(). Bu durum aykırı değerlerin tahminlerimiz üzerine olan etkisini büyük ölçüde azaltacaktır ve haftanın gününü örneğini kaldırmak için iyi bir iş çıkaran bir model sunar.
mod3 <- MASS::rlm(n ~ wday * term, data = daily)
daily %>%
add_residuals(mod3, "resid") %>%
ggplot(aes(date, resid)) +
geom_hline(yintercept = 0, size = 2, colour = "white") +
geom_line()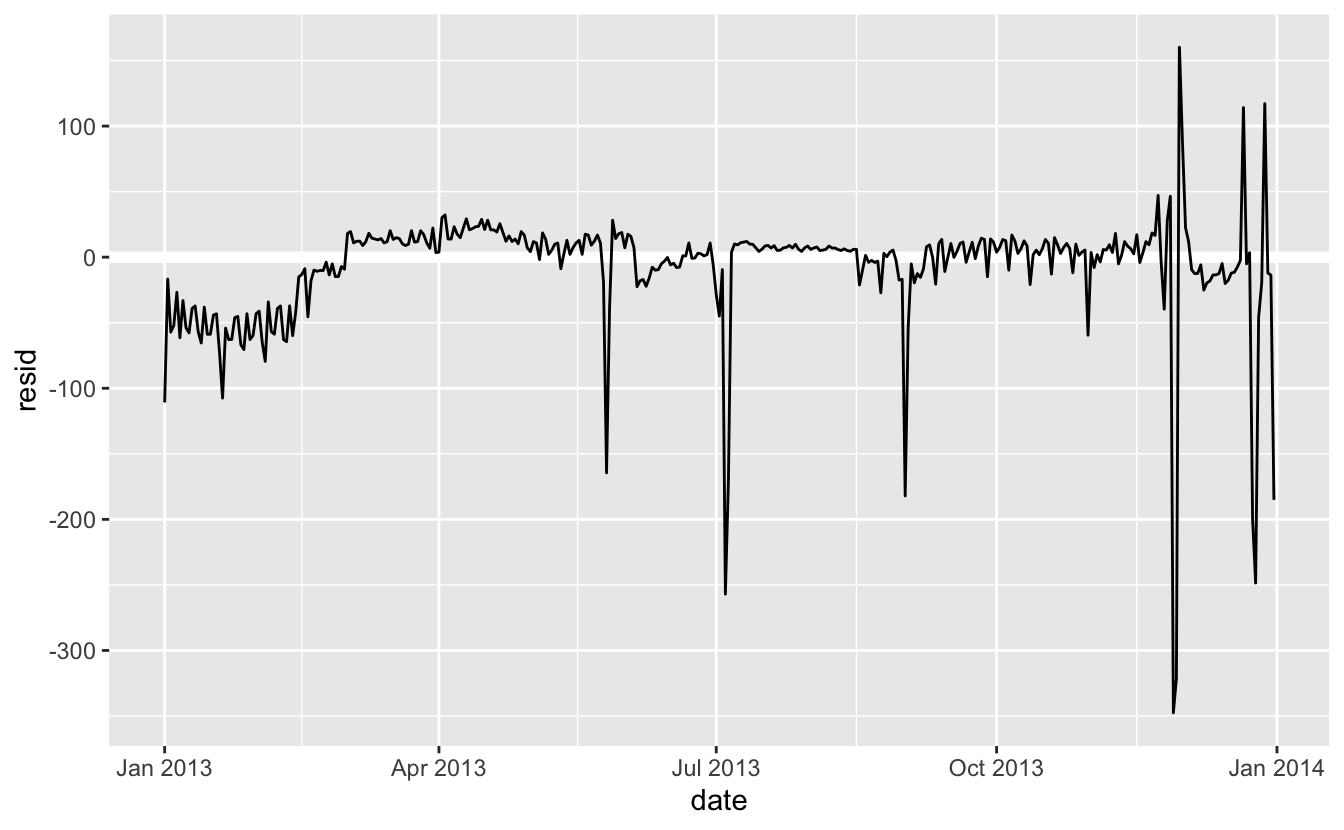
Uzun vadeli eğilim ile pozitif ve negatif aykırı değerleri görmek artık çok daha kolay.
24.3.3 Hesaplanan değişkenler
Eğer birçok model ve görselleştirme ile uğraşıyorsanız, oluşturulan değişkenleri bir fonksiyon içerisinde toplamak iyi bir fikirdir, böylece farklı yerlerde farklı dönüşümlerin kazara uygulanma şansını ortadan kaldırmış olursunuz. Örneğin, şu şekilde bir şey yazabiliriz:
compute_vars <- function(data) {
data %>%
mutate(
term = term(date),
wday = wday(date, label = TRUE)
)
}Başka bir seçenek de dönüşümleri doğrudan model formülü içerisine koymaktır:
wday2 <- function(x) wday(x, label = TRUE)
mod3 <- lm(n ~ wday2(date) * term(date), data = daily)Her iki yaklaşım da makuldur. Şayet çalışmanızı kontrol etmek veya görsel amaçlı kullanmak istiyorsanız, dönüştürülmüş değişkeni görünür kılmak kullanışlıdır. Ancak, birden çok kez sütun döndüren dönüşümlwei (spline’lar gibi) kolayca kullanamazsınız. Model fonksiyonu içerisine dönüşümleri dahil etmek, birçok veri kümesiyle çalışırken işinizi nispeten kolaylaştırır çünkü modelin kendi içerisinde mevcuttur.
24.3.4 Yılın zamanı: Alternatif bir yaklaşım
Önceki bölümde, modeli geliştirmek için alan bilgimizi (ABD okulllarının seyahatleri nasıl etkilediği) kullandık. Bilgimizi açıkca model üzerinde kullanmanın bir alternatifi, verilere daha fazla ifade imkanı tanımaktır. Daha esnek bir model kullanabilir ve ilgilendiğimiz tasarımı yakalamasına izin verebiliriz. Basit bir lineer eğilim yeterli değildir, bu nedenle doğal bir eğri kullanmayı deneyerek tüm yıla uygun eğim uydurabiliriz.
library(splines)
mod <- MASS::rlm(n ~ wday * ns(date, 5), data = daily)
daily %>%
data_grid(wday, date = seq_range(date, n = 13)) %>%
add_predictions(mod) %>%
ggplot(aes(date, pred, colour = wday)) +
geom_line() +
geom_point()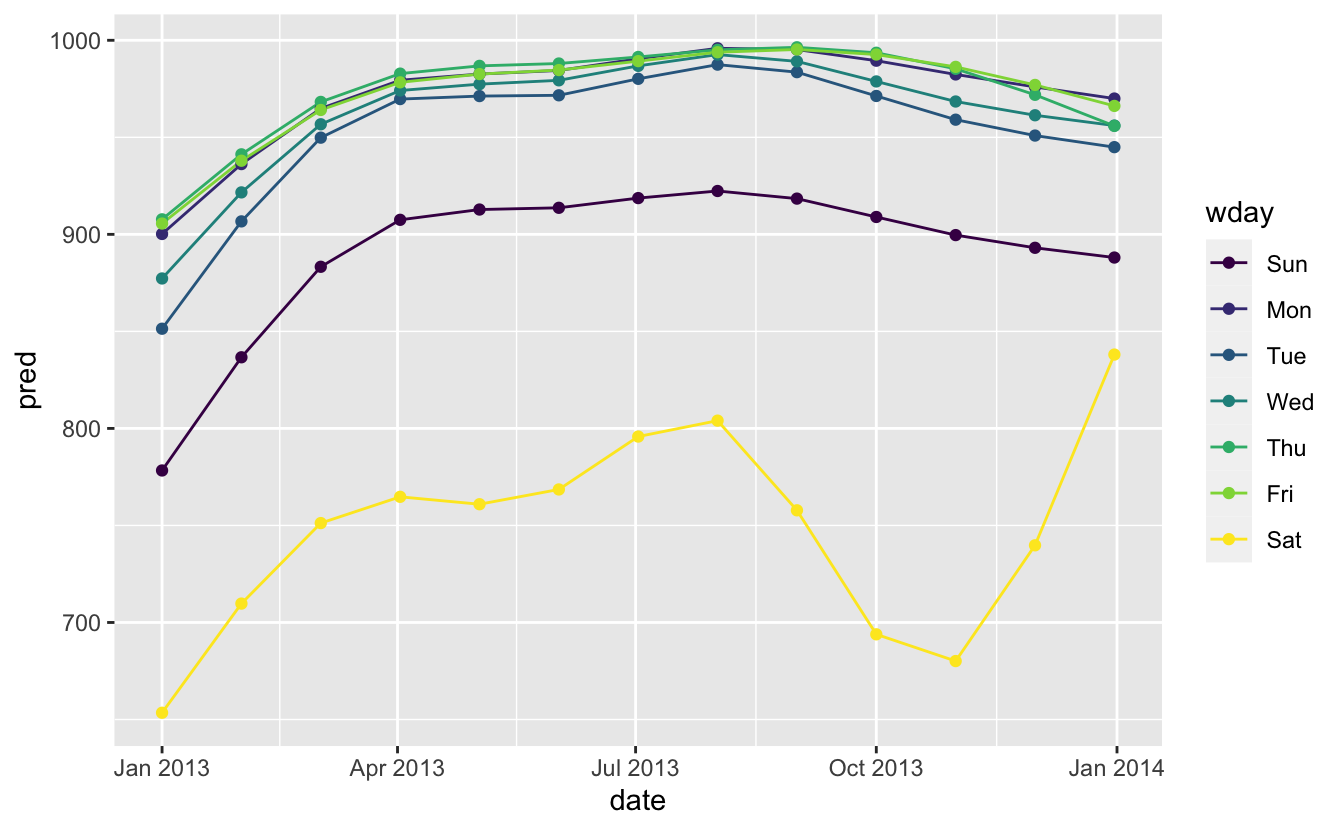
Cumartesi uçuşlarının sayısında güçlü bir işaret görüyoruz. Bu bize güven vermektedir. Çünkü ham verilerde de bu şekli gördük. Aynı sonuçları farklı yaklaşımlardan alıyor olmanız iyi bir işarettir.
24.3.5 Uygulamalar
Google’da araştırma becerilenizie kullanrak 20 Ocak, 26 Mayıs ve 1 Eylül’de neden beklenenden daha az uçuş olduğunu beyin fırtınası yapınız. (İpucu: Hepsi aynı açıklamaya sahip.) Bu günler başka bir yıla nasıl genelleştirilir?
Yüksek pozitif rezidüelleri olan bu üç gün neyi temsil eder? Bu günler başka bir yıla nasıl genelleştirilir?
daily %>% top_n(3, resid) #> # A tibble: 3 × 5 #> date n wday resid term #> <date> <int> <ord> <dbl> <fct> #> 1 2013-11-30 857 Sat 112. sonbahar #> 2 2013-12-01 987 Sun 95.5 sonbahar #> 3 2013-12-28 814 Sat 69.4 sonbaharwdaydeğişkenini terimlere ayıran yeni bir değişken oluşturun, ancak sadece Cumartesileri için, örneğinPerş,Cum, fakatCts-yaz,Cts-bahar,Cts-sonbaharşeklinde olsun. Bu modelwdayveterm’in her bir kombinasyonunu içeren model ile nasıl karşılaştırılır?Cumartesiler için bir terim, resmi tatiller ve haftanın günlerini birleştiren yeni bir
wdaydeğişkeni oluşturun. Bu modelin rezidüelleri nasıl gözükür?Aya göre değişen bir haftanın gününe uygularsanız nasıl etkilenir? (örneğin,
n~wday*ay)? Bu neden pek yardımcı olmaz?n~wday + ns(date,5)şeklinde bir model nasıl görünmesini beklersiniz? Veriler hakkındaki neyi bildiğinizi bilmenin, neden bu kadar etkili olmayacağını umuyorsunuz?Pazar gününden ayrılan insanların daha çok Pazartesi günü için iş seyahati yaptıklarının muhtemel olduğunu varsaydık. Zaman ve mesafeye bağlı olarak nasıl ayrım gösterdiğini görerek bu hipotezi ortaya koyun: eğer doğruya, Pazar akşamı uçuşlarının daha uzaktaki yerlere olduğunu görmeyi beklersiniz.
Cumartesi ve Pazar günlerinin grafikte ayrı uçlarda olması biraz sinir bozucu. Faktör seviyelerini ayarlamak için ufak bir fonksiyon yazın ki böylece hafta Pazartesi ile başlasın.
24.4 Modeller hakkında daha fazla öğrenin
Biz sadece modellemenin yüzeyine ufak bir çentik attık, ancak umarım kendi veri analizlerinizi geliştirmek için kullanabileceğiniz bazı basit, ancak genel amaçlı araçlar elde etmişsinizdir. Kolaydan başlamakta hiçbir sorun yoktur! Gördüğünüz gibi, çok basit modeller bile değişkenler arasındaki etkileşimi azaltma yeteneğinizde çarpıcı bir fark yaratabilir.
Bu modelleme ile ilgili bölümler, kitabın geri kalanına göre daha çok sabit fikirler içermektedir. Modellemeye, diğerlerinden biraz farklı bir bakış açısıyla yaklaşıyorum ve buna ayırabildiğim nispeten az yer var. Sadece modelleme aslında kendi üzerine bir kitabı hak ediyor, bu yüzden bu üç kitaptan en az birini okumanızı şiddetle tavsiye ederim:
Statistical Modeling: A Fresh Approach Yazar: Danny Kaplan, http://www.mosaic-web.org/go/StatisticalModeling/. Bu kitap, sezginizi, matematiksel araçlarınızı ve R becerilerinize paralel olarak geliştirdiğiniz modellemeye nazik bir giriş sağlar. Kitap, güncel ve veri bilimi ile ilgili bir müfredat sağlayarak, geleneksel bir “istatistiğe giriş” dersinin yerini alımaktadır.
An Introduction to Statistical Learning Yazarlar: Gareth James, Daniela Witten, Trevor Hastie, ve Robert Tibshirani, http://www-bcf.usc.edu/~gareth/ISL/ (çevrimiçi ücretsiz olarak ulaşılabilir). Bu kitap istatistiksel öğrenme olarak bilinen güncel modelleme teknikleri ailesini topluca sunmaktadır. Modellerin arkasında yatan matematiği daha derinden kavramak için, Trevor Hastie, Robert Tibshirani ve Jerome Friedman tarafından yazılmış bir klasik olan Elements of Statistical Learning https://web.stanford.edu/~hastie/Papers/ESLII.pdf okuyun (bu kaynağa da çevrimiçi ücretsiz ulaşılabilir).
Applied Predictive Modeling Yazarlar: Max Kuhn and Kjell Johnson. Bu kitap caret paketiyle ilgili uygulamaları içerir. Gerçek hayata dair modelleri yordamlama zorluklarıyla ilgili pratik araçlar sağlar. http://appliedpredictivemodeling.com.