7 Keşifsel veri analizi
7.1 Giriş
Bu bölümde verinizi sistematik şekilde keşfetmek için görselleştirme ve dönüştürmeyi nasıl kullanacağınız anlatılmaktadır. Bu işlemi istatistikçiler keşifsel veri analizi veya kısaca KVA (Exploratory Data Analysis, EDA) olarak adlandırır. KVA tekrarlı bir döngüdür:
Veriniz hakkında sorular oluşturursunuz.
Verinizi görselleştirerek, dönüştürerek ve modelleyerek cevaplar ararsınız.
Sorularınızı geliştirmek ve/veya yeni sorular üretmek için öğrendiklerinizi kullanırsınız.
KVA katı kuralları olan resmi bir süreç değildir. KVA her şeyden çok bir düşünüş tarzıdır. KVA’nın ilk başlarında aklınıza gelen her fikri araştırmakta özgür hissetmelisiniz. Bu fikirlerden bazıları meyve verirken diğerleri solup gidecektir. Keşfiniz devam ettikçe, sonunda yazıp başkalarıyla paylaşacağınız belirli üretken alanlara yöneleceksiniz.
Sorular size bir tabakta sunulsa bile KVA her veri analizinin önemli bir bölümüdür çünkü her zaman verinizin kalitesini incelemeye ihtiyaç duyarsınız. Veri temizleme KVA uygulamalarından sadece biridir. Verinizin beklentileri karşılayıp karşılamadığını sorarsınız. Veri temizlemek için bütün KVA araçlarını kullanmanız gerekir: görselleştirme, dönüştürme ve modelleme.
7.2 Sorular
“Rutin istatistiksel sorular yoktur, sadece sorgulanabilir istatistiksel rutinler vardır.” — Sir David Cox
“Doğru bir soruya çoğu zaman belirsiz olan yaklaşık bir cevap, yanlış bir soruya her zaman kesin hale getirilebilen tam bir cevaptan yeğdir.” — John Tukey
KVA sırasında amacınız veriniz hakkında bir anlayış geliştirmektir. Bunu yapmanın en kolay yolu, araştırmanıza rehberlik edecek sorular kullanmaktır. Soru sorduğunuzda soru, dikkatinizi veri setininizin belirli bir bölgesine toplar ve hangi grafikler, modeller veya dönüşümleri yapacağınıza karar vermenize yardımcı olur.
KVA esasen yaratıcı bir süreçtir. Çoğu yaratıcı süreç gibi kaliteli sorular sormanın yolu çok miktarda soru üretmekten geçer. Veri setinizde ne gibi içgörüler olduğunu bilmediğinizden analizinizin başlangıcında açıklayıcı sorular sormak zordur. Diğer taraftan sorduğunuz her yeni soru size verinizin başka bir yönünü gösterecektir ve keşif yapma şansınızı artıracaktır. Her soruyu, bulduklarınıza dayanarak yeni bir soruyla takip ettiğinizde verinizin en ilginç kısımlarına hızlıca dalabilir ve bir dizi düşünceyi tetikleyen sorular geliştirebilirsiniz.
Araştırmanıza rehberlik etmesi için hangi soruları soracağınıza dair hiçbir kural yoktur. Ancak verinizde keşifler yapmak için iki tip soru her zaman faydalı olacaktır. Genel olarak bu soruları şu şekilde ifade edebilirsiniz:
Değişkenlerimde ne tür bir varyasyon var?
Değişkenlerim arasında ne tür bir kovaryasyon var?
Bu bölümün geri kalanı bu iki soruya odaklanacaktır. Varyasyon ve kovaryasyonun ne olduğunu açıklayacağım ve her soruya cevap vermenin çeşitli yollarını göstereceğim. Tartışmayı kolaylaştırmak için bazı terimleri açıklayalım:
değişken ölçebileceğiniz bir miktar, nitelik veya özelliktir.
değer ölçtüğünüzde değişkenin durumudur. Değişkenin durumu ölçümden ölçüme değişebilir.
gözlem benzer koşullar altında yapılan ölçüm dizisidir. (genelde bir gözlemdeki ölçümlerin hepsini aynı zamanda ve aynı nesenede yaparsınız). Gözlem her biri farklı bir değişkenle ilişkili çeşitli değerler içerir. Gözlemi bazen veri noktası olarak adlandıracağım.
tablo şeklinde veri her biri bir değişken ve bir gözlemle ilişkili bir değerler dizisidir. Her değer kendi “hücresine” yerleştirilmişse, her değişken kendi sütununda ve her gözlem kendi sırasındaysa veri tablo şeklinde tidy olur (düzenlidir).
Şu ana kadar gördüğünüz bütün veriler düzenliydi. Gerçek hayatta verilerin çoğu düzenli değildir bu nedenle düzenli veri kısmında bu fikirlere geri döneceğiz.
7.3 Varyasyon
Varyasyon bir değişkendeki değerlerin ölçümden ölçüme değişme eğilimidir. Varyasyonu gerçek yaşamda kolaylıkla görebilirsiniz. Herhangi bir sürekli değişkeni iki kere ölçerseniz iki farklı sonuç alırsınız. Işığın hızı gibi sabit değerleri ölçtüğünüzde de bu geçerlidir. Ölçümlerinizin her biri ölçümden ölçüme farklılık gösteren küçük bir miktar hata içerecektir. Kategorik değişkenler farklı denekler (örn. farklı kişilerin göz renkleri) veya farklı zamanlarda (örn. farklı anlarda bir elektronun enerji düzeyleri) ölçtüğünüzde de değişkenlik gösterebilir. Her değişken ilginç bilgiler ortaya çıkarabilen kendi varyasyon örüntüsüne sahiptir. Bu örüntüyü anlamanın en iyi yolu değişkenin değerlerinin dağılımını görselleştirmektir.
7.3.1 Dağılımları görselleştirme
Bir değişkenin dağılımını nasıl görselleştireceğiniz değişkenin kategorik mi yoksa sürekli mi olduğuna bağlıdır. Bir değişken, küçük bir değer dizisinden sadece birini alabiliyorsa kategoriktir. R’da kategorik değişkenler genellikle faktörler veya karakter vektörleri olarak kaydedilir. Bir kategorik değişkenin dağılımını incelemek için çubuk grafik kullanın:
ggplot(data = diamonds) +
geom_bar(mapping = aes(x = cut))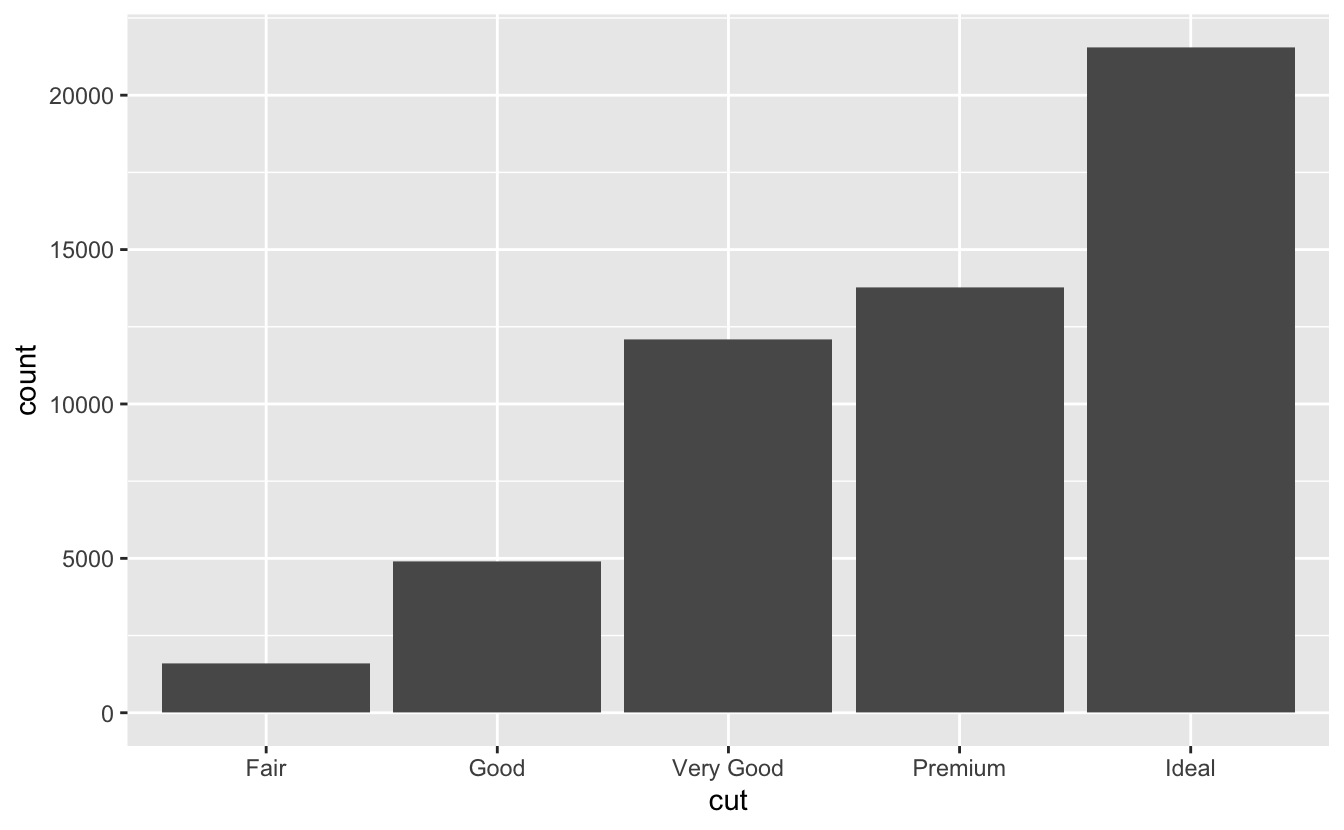
Çubukların yüksekliği her x değeri ile kaç gözlem olduğunu gösterir. Bu değerleri elle dplyr::count()ile hesaplayabilirsiniz:
diamonds %>%
count(cut)
#> # A tibble: 5 × 2
#> cut n
#> <ord> <int>
#> 1 Fair 1610
#> 2 Good 4906
#> 3 Very Good 12082
#> 4 Premium 13791
#> 5 Ideal 21551Sıralı değerlerden oluşan sonsuz bir dizi alabiliyorsa değişken süreklidir. Sayılar ve tarih ve zamanlar sürekli değişkenlere iki örnektir. Sürekli değişkenin dağılımını incelemek için histogram kullanın:
ggplot(data = diamonds) +
geom_histogram(mapping = aes(x = carat), binwidth = 0.5)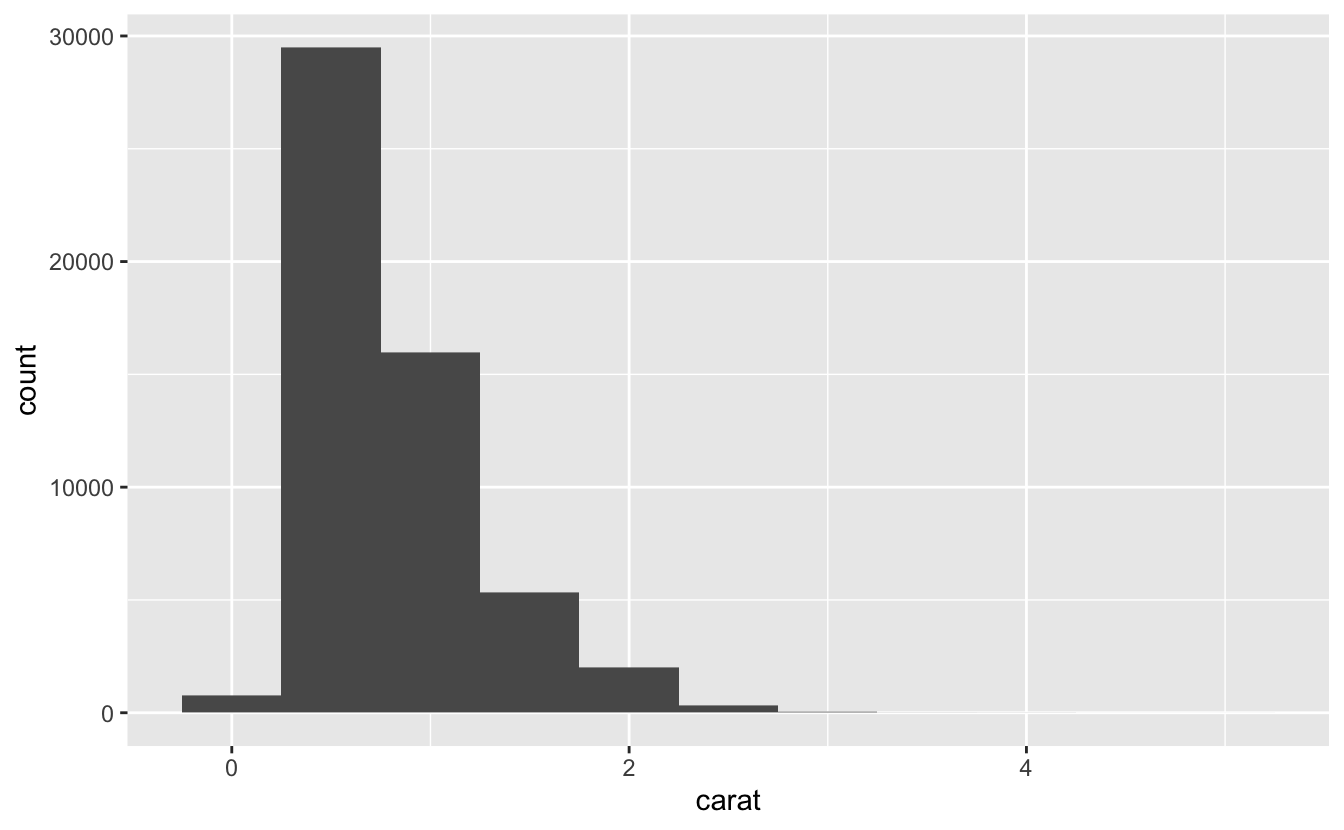
Bunu elle dplyr::count() ve ggplot2::cut_width()i birleştirerek hesaplayabilirsiniz:
diamonds %>%
count(cut_width(carat, 0.5))
#> # A tibble: 11 × 2
#> `cut_width(carat, 0.5)` n
#> <fct> <int>
#> 1 [-0.25,0.25] 785
#> 2 (0.25,0.75] 29498
#> 3 (0.75,1.25] 15977
#> 4 (1.25,1.75] 5313
#> 5 (1.75,2.25] 2002
#> 6 (2.25,2.75] 322
#> # … with 5 more rowsHistogram x eksenini eşit aralıklı gruplara böler ve her gruba düşen gözlem sayısını göstermek için çubuğun yüksekliğini kullanır. Yukarıdaki grafikte en uzun çubuk neredeyse 30.000 gözlemin, çubuğun sağ ve sol kenarları olan 0,25 ve 0,75 arası bir ‘carat’ (karat) değerine sahip olduğunu göstermiştir.
Bir histogramdaki aralıkların genişliğini x değişkeni birimlerinde ölçülen binwidth(grup genişliği) argümanı ile belirleyebilirsiniz. Histogramlarla çalışırken daima çeşitli grup genişliklerini araştırmalısınız çünkü farklı grup genişlikleri farklı örüntüler ortaya çıkarabilir. Örneğin, sadece üç karattan küçük boyuttaki elmaslara odaklandığımızda ve daha küçük bir grup genişliği seçtiğimizde yukarıdaki grafik şöyle görünür:
smaller <- diamonds %>%
filter(carat < 3)
ggplot(data = smaller, mapping = aes(x = carat)) +
geom_histogram(binwidth = 0.1)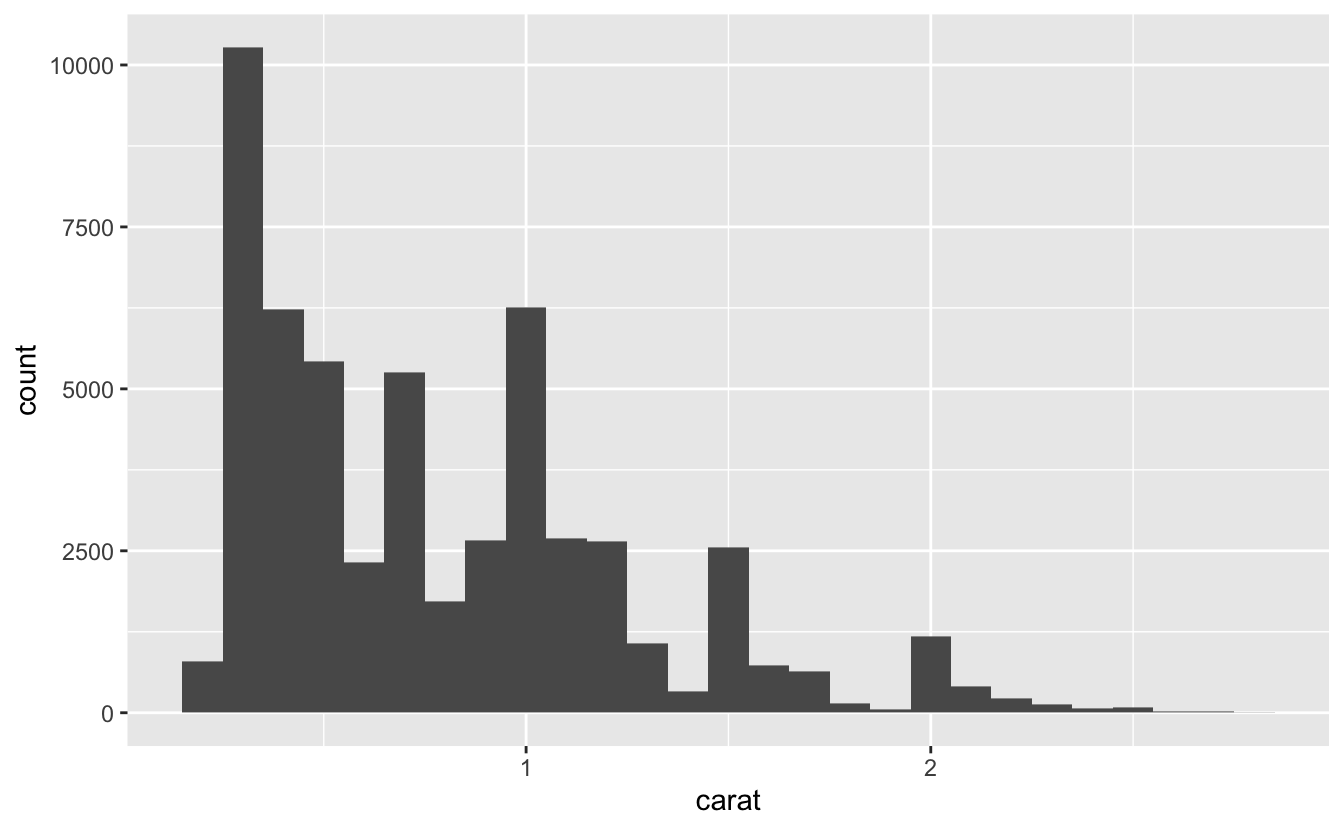
Birden çok histogramı aynı grafiğe yerleştirmek isterseniz geom_histogram()yerine geom_freqpoly() kullanmanızı tavsiye ederim. geom_freqpoly() , geom_histogram()ile aynı hesaplamaları yapar fakat sayımları çubuklarla göstermek yerine çizgileri kullanır. Çakışan çizgileri anlamak çakışan çubukları anlamaktan daha kolaydır.
ggplot(data = smaller, mapping = aes(x = carat, colour = cut)) +
geom_freqpoly(binwidth = 0.1)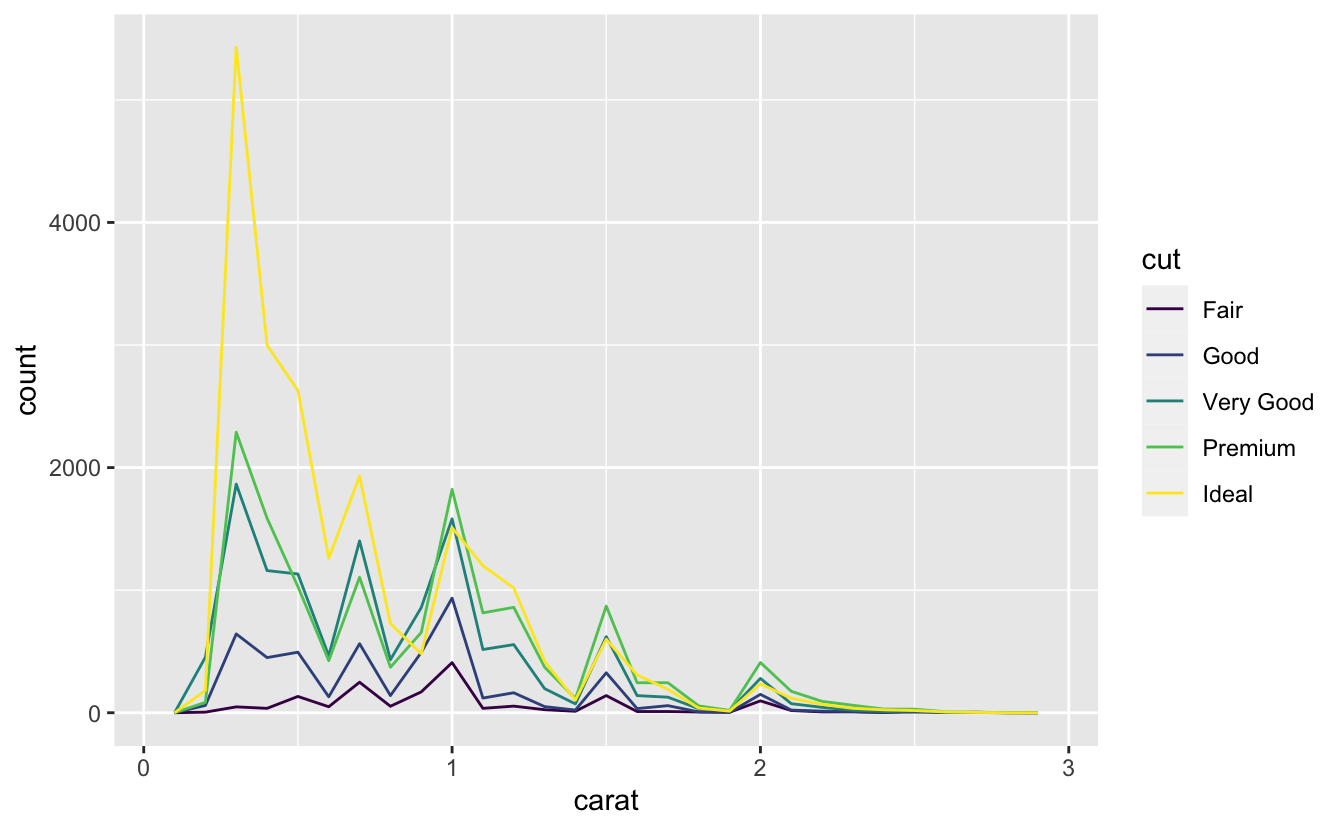
Bu tür grafikle ilişkili bir kaç güçlük vardır. Bunlara kategorik ve sürekli değişkenleri görselleştirme bölümünde değineceğiz.
Şimdi varyasyonu görselleştirebildiğinize göre, grafiklerinizde neyi aramalısınız? Ve ne tür takip soruları sormalısınız? Grafiklerinizde bulacağınız en faydalı türde bilgilerin bir listesinin yanı sıra her türde bilgi için bazı takip sorularını bir araya getirdim. İyi takip soruları sormanın püf noktası merakınıza (daha fazla neyi öğrenmek istersiniz) ve şüpheciliğinize (bu nasıl yanıltıcı olabilir) güvenmektir.
7.3.2 Tipik değerler
Hem çubuk grafik hem de histogramlarda, uzun çubuklar bir değişkenin yaygın değerlerini ve daha kısa çubuklar daha az yaygın değerlerini gösterir. Çubuk olmayan yerler verinizde görülmeyen değerleri ortaya çıkarırlar. Bu bilgiyi faydalı sorulara dönüştürmek için beklenmedik her şeyi araştırın:
Hangi değerler en yaygın? Neden?
Hangi değerler nadir? Neden?
Herhangi bir sıradışı örüntü görebiliyor musunuz? Bunun açıklaması ne olabilir?
Örnek olarak, aşağıdaki histogram çeşitli ilginç sorular göstermektedir:
Neden tam karatlarda ve yaygın karat fraksiyonlarında daha fazla elmas var?
Neden her yükseltinin biraz sağında, her yükseltinin biraz solunda olduğundan daha fazla elmas var?
Neden 3 karattan büyük hiç elmas yok?
ggplot(data = smaller, mapping = aes(x = carat)) +
geom_histogram(binwidth = 0.01)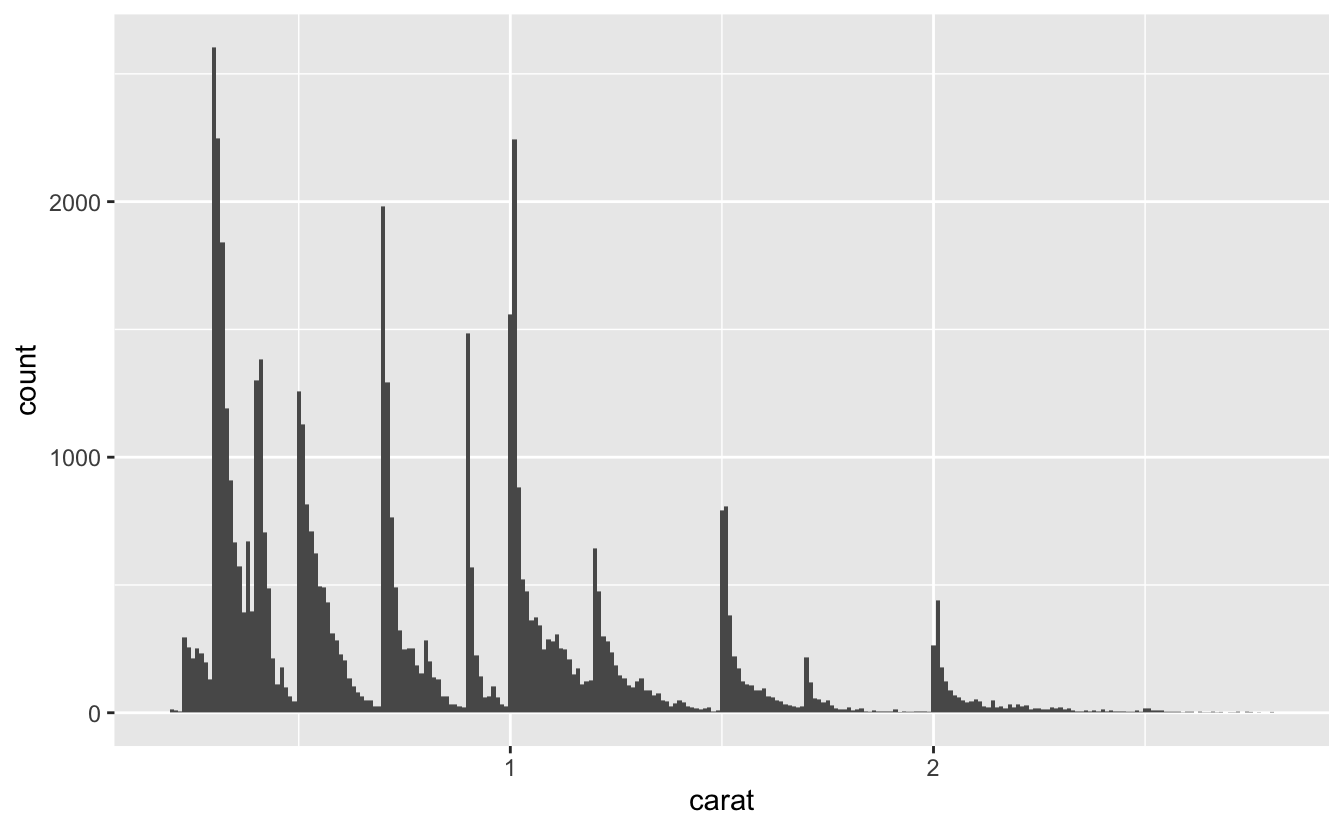
Benzer değerlerden oluşan kümeler verinizde alt gruplar olduğunu gösterir. Alt grupları anlamak için şu soruları sorun:
Her küme içerisindeki gözlemler birbirine nasıl benzerlik gösteriyor?
Ayrı kümelerdeki gözlemler birbirinden nasıl farklılık gösteriyor?
Kümeleri nasıl açıklar veya tarif edersiniz?
Kümelerin görünümü neden yanıltıcı olabilir?
Aşağıdaki histogram Yellowstone Milli Parkı’nda Old Faithful Geyser’in 272 patlamasının uzunluğunu (dakika cinsinden) göstermektedir. Patlama süreleri iki gruba ayrılıyor gibi görünmektedir: kısa patlamalar (yaklaşık 2 dakika) ve uzun patlamalar (4-5 dakika) ve ikisinin arasında çok az patlama vardır.
ggplot(data = faithful, mapping = aes(x = eruptions)) +
geom_histogram(binwidth = 0.25)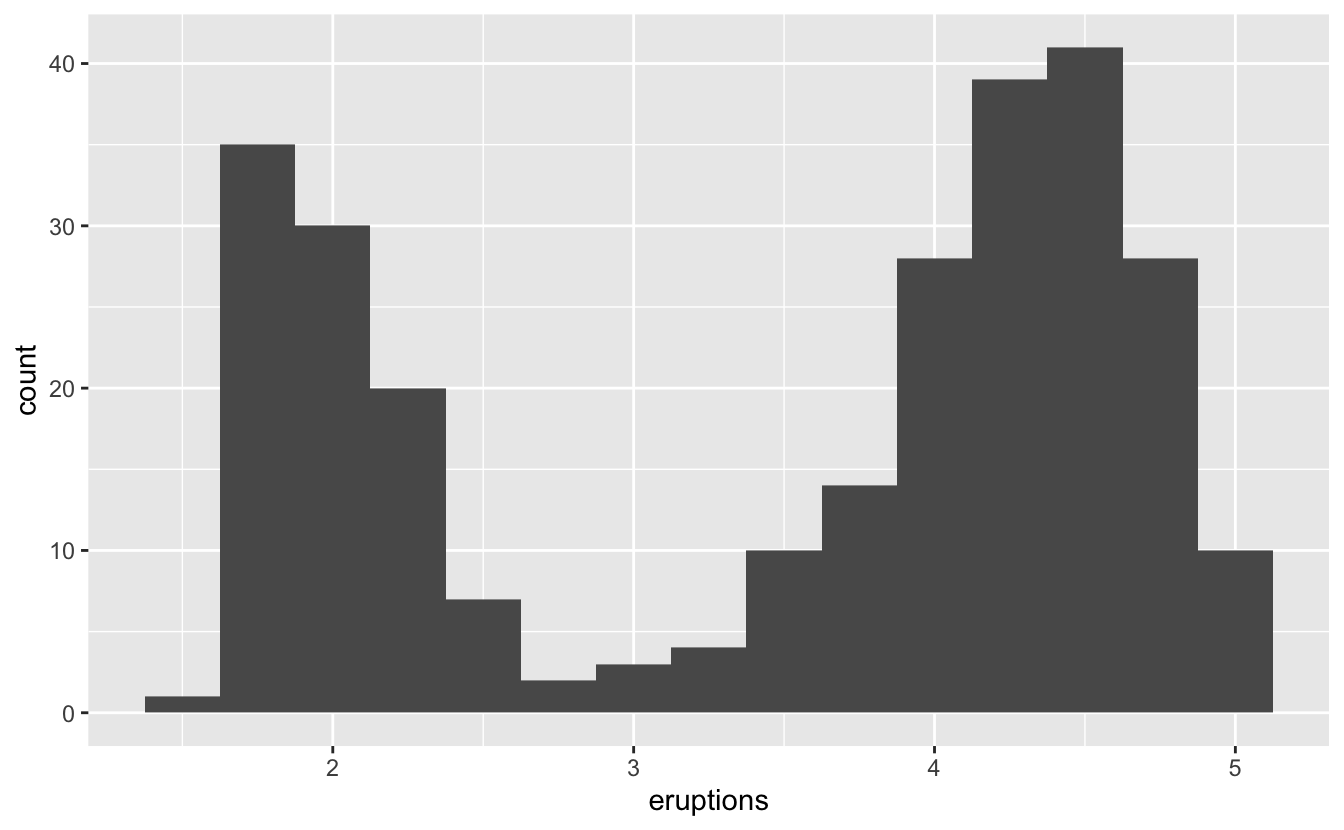
Yukarıdaki sorulardan çoğu bir değişkenin değerinin başka bir değişkenin davranışını açıklayıp açıklayamayacağını görmek gibi değişkenler arasında bir ilişki olup olmadığını araştırmanızı teşvik edecektir. Bu konuya geleceğiz.
7.3.3 Sıradışı değerler
Uç değerler sıradışı değerlerdir; örüntüye uyuyor gibi görünmeyen veri noktalarıdır. Bazen uç değerler veri girme hatalarıdır; bazen önemli yeni bilime işaret ederler. Çok veriniz olduğunda uç değerleri histogramda görmek zordur. Örneğin elmas veri setinden y değişkeninin dağılımını alın. Uç değerlerin tek kanıtı x eksenindeki sıradışı genişlikte sınırlardır.
ggplot(diamonds) +
geom_histogram(mapping = aes(x = y), binwidth = 0.5)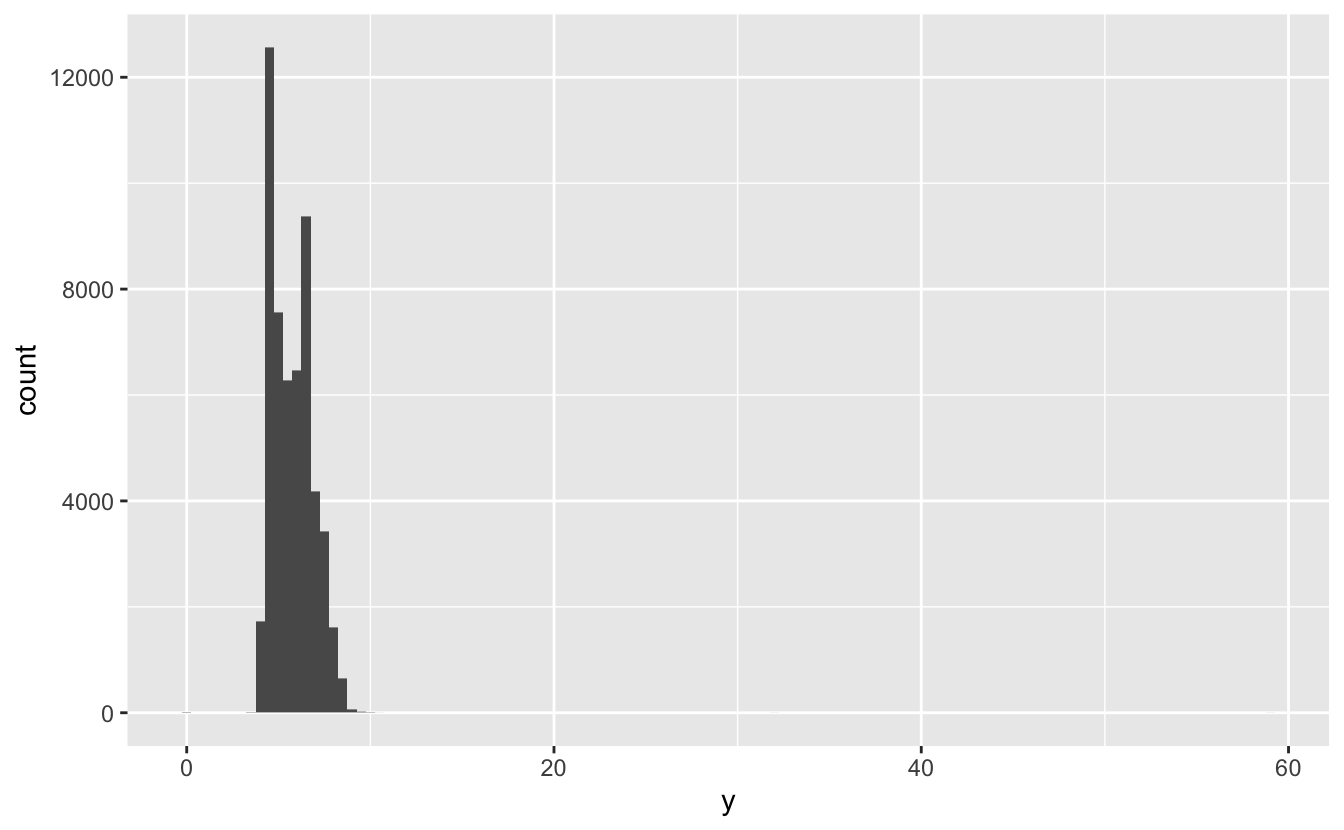
Yaygın gruplarda o kadar çok gözlem vardır ki, nadir gruplar çok kısadır ve göremezsiniz (ancak 0’a dikkatle bakarsanız belki birşey görebilirsiniz). Olağandışı değerleri görmeyi kolaylaştırmak için coord_cartesian() ile y ekseninin küçük değerlerine odaklanmalıyız:
ggplot(diamonds) +
geom_histogram(mapping = aes(x = y), binwidth = 0.5) +
coord_cartesian(ylim = c(0, 50))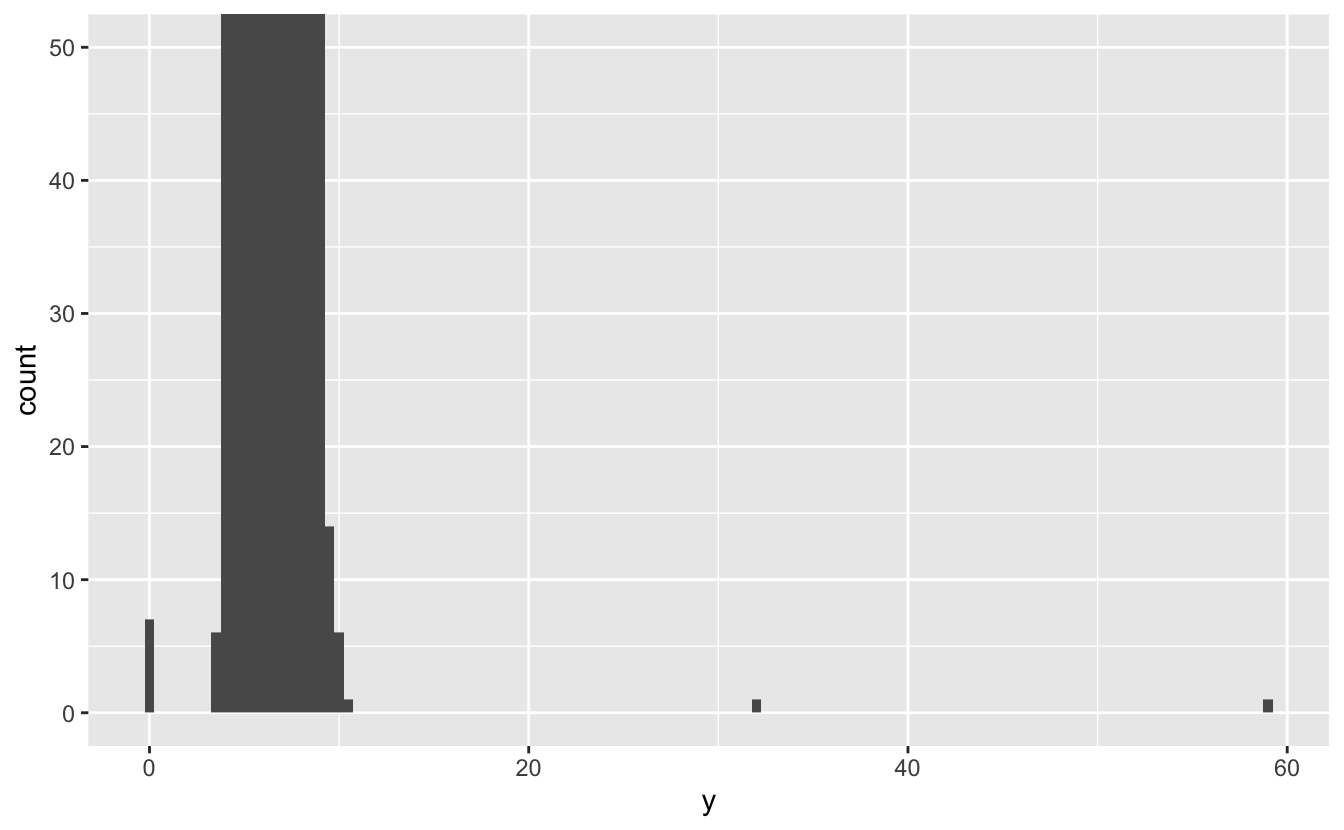
(coord_cartesian() aynı zamanda x eksenine yakınlaşmanız gerektiğinde kullanmanız için xlim() argümanına sahiptir. ggplot2 de biraz farklı çalışan xlim() ve ylim() fonksiyonlarına sahiptir: sınırların dışındaki verileri atarlar.)
Bu, üç sıradışı değer olduğunu görmemize olanak tanır: 0, ~30 ve ~60. Bunları dplyr ile çıkarırız:
unusual <- diamonds %>%
filter(y < 3 | y > 20) %>%
select(price, x, y, z) %>%
arrange(y)
unusual
#> # A tibble: 9 × 4
#> price x y z
#> <int> <dbl> <dbl> <dbl>
#> 1 5139 0 0 0
#> 2 6381 0 0 0
#> 3 12800 0 0 0
#> 4 15686 0 0 0
#> 5 18034 0 0 0
#> 6 2130 0 0 0
#> 7 2130 0 0 0
#> 8 2075 5.15 31.8 5.12
#> 9 12210 8.09 58.9 8.06ydeğişkeni bu elmasların üç boyutundan birini mm cinsinden ölçer. Elmasın 0 mm çapa sahip olmayacağını biliyoruz bu nedenle bu değerler hatalı olmalıdır. 32 mm ve 59 mm ölçümlerinin de mantıksız olduğundan şüphe edebiliriz: bu elmaslar bir inçten uzun ancak yüzbinlerce dolar etmiyorlar!
Analizi uç değerler ile ve uç değerler olmadan tekrar etmek iyi bir uygulamadır. Sonuçlar üzerindeki etkisi minimum ise ve neden orada olduklarını anlayamıyorsanız bunların yerine eksik değer koyarak devam etmek makuldur. Ancak sonuçlarınız üzerinde önemli bir etkiye sahiplerse gerekçe olmadan bunları atmamalısınız. Bunlara neyin sebep olduğunu bulmalısınız (örn. veri giriş hatası) ve raporunuzda bunları çıkardığınızı bildirmelisiniz.
7.3.4 Alıştırmalar
diamondsda (elmaslar)x,yvezdeğişkenlerinin herbirinin dağılımını inceleyin. Ne öğrenirsiniz? Bir elmas düşünün ve hangi boyutun uzunluk, genişlik ve derinlik olduğuna nasıl karar verebileceğinizi düşünün.price(fiyat) dağılımını inceleyin. Sıradışı veya şaşırtıcı bir şey keşfettiniz mi? (İp ucu:binwidth(grup genişliği) dikkatlice düşünün ve geniş bir değer aralığı denediğinizden emin olun.)Kaç tane elmas 0,99 karat? Kaç tanesi 1 karat? Farklılığın nedeninin ne olduğunu düşünüyorsunuz?
Bir histograma yakınlaşırken
coord_cartesian()ilexlim()veyaylim()i karşılaştırıp kıyaslayın.binwidthi ayarlamadan bırakırsanız ne oluyor? Bir çubuğun sadece yarısı görünecek şekilde yakınlaşınca ne oluyor?
7.4 Eksik değerler
Veri setinizde sıradışı değerlerle karşılaştıysanız ve analizin geri kalanına ilerlemek istiyorsanız iki seçeneğiniz var.
Tuhaf değerler olan bütün sırayı çıkarın:
diamonds2 <- diamonds %>% filter(between(y, 3, 20))Bu seçeneği önermiyorum çünkü sadece bir ölçümün geçersiz olması bütün ölçümlerin geçersiz olduğu anlamına gelmez. Ayrıca, düşük kaliteli bir veriye sahipseniz her değişkene bu yaklaşımı uyguladığınızda hiç veriniz kalmayabilir!
Bunun yerine sıradışı değerleri eksik değerler ile değiştirmenizi tavsiye ediyorum. Bunu yapmanın en kolay yolu değişkenin yerine değiştirilmiş bir kopyasını koymak için
mutate()kullanmaktır. Sıradışı değerleriNAile değiştirmek içinifelse()fonksiyonunu kullanabilirsiniz:diamonds2 <- diamonds %>% mutate(y = ifelse(y < 3 | y > 20, NA, y))
ifelse() üç argümana sahiptir. İlk argüman test mantıklı bir vektör olmalıdır. test TRUE olduğunda sonuç ikinci argümanın değerini, yes, ve false olduğunda ve üçüncü argümanın değerini,no, içerecektir. ifelse fonksiyonuna alternatif olarak dplyr::case_when()kullanın. Mevcut değişkenlerin karmaşık bir kombinasyonuna dayalı olan yeni bir değişken yaratmak istediğinizde mutate içindeki case_when() özellikle kullanışlıdır.
ggplot2 de R gibi eksik değerlerin asla sessizce eksik kalmaması gerektiği felsefesine dayalıdır. Eksik değerleri nerede grafiğe aktarmanız gerektiği açık değildir, bu yüzden ggplot2 grafikte bunları içermez ancak çıkarıldıklarına dair uyarı verir:
ggplot(data = diamonds2, mapping = aes(x = x, y = y)) +
geom_point()
#> Warning: Removed 9 rows containing missing values (geom_point).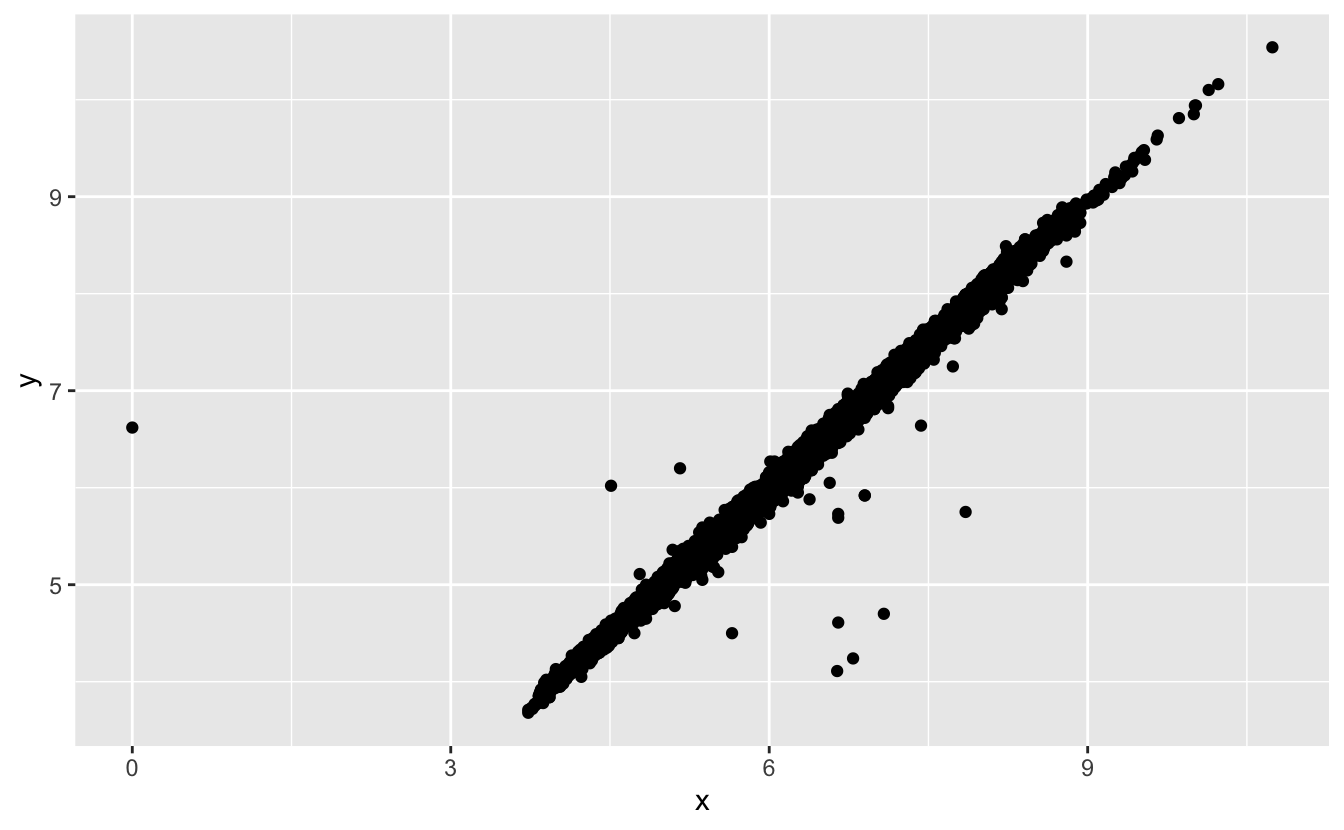
Bu uyarıyı ortadan kaldırmak için na.rm = TRUE olarak ayarlayın:
ggplot(data = diamonds2, mapping = aes(x = x, y = y)) +
geom_point(na.rm = TRUE)Başka bir zaman eksik değerler olan gözlemlerin kayıtlı değerler olan gözlemlerden farkını anlamak isteyebilirsiniz. Örneğin, nycflights13::flightsda, dep_time değişkenindeki eksik değerler uçuşun iptal edildiğini gösterir. Bu yüzden iptal edilen ve iptal edilmeyen zamanlarda planlanan uçuş zamanlarını karşılaştırmak isteyebiliriniz. Bunu is.na() ile yeni bir değişken yaparak yapabilirsiniz.
nycflights13::flights %>%
mutate(
cancelled = is.na(dep_time),
sched_hour = sched_dep_time %/% 100,
sched_min = sched_dep_time %% 100,
sched_dep_time = sched_hour + sched_min / 60
) %>%
ggplot(mapping = aes(sched_dep_time)) +
geom_freqpoly(mapping = aes(colour = cancelled), binwidth = 1/4)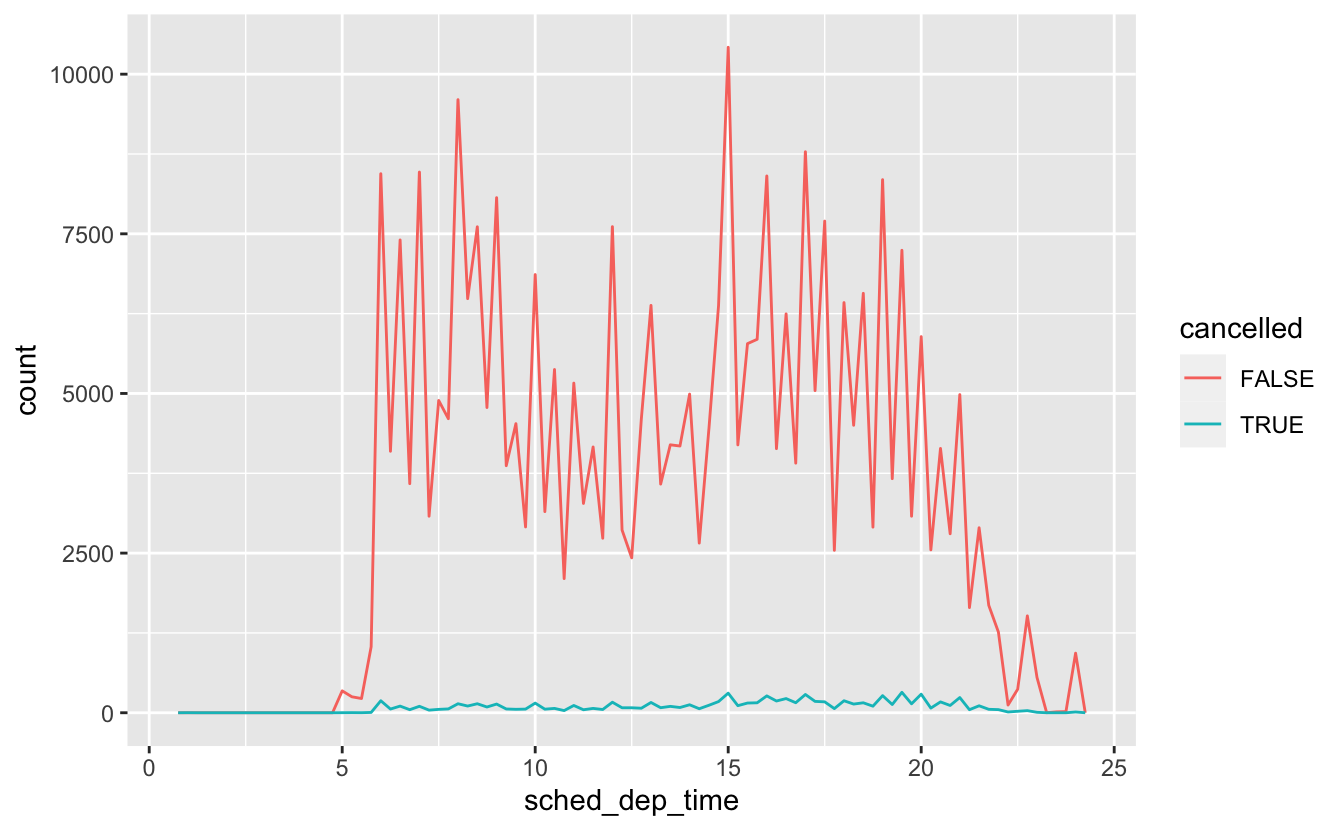
Ancak bu grafik harika değil çünkü iptal edilen uçuşlardan çok daha fazla iptal edilmeyen uçuş var. Bir sonraki bölümde bu karşılaştırmayı geliştirmek için kullanabileceğiniz bazı teknikleri inceleyeceğiz.
7.5 Kovaryasyon
Varyasyon bir değişken içerisindeki davranışı açıklıyorsa, kovaryasyon değişkenler arasındaki davranışı açıklar. Kovaryasyon iki veya daha fazla değişkenin değerlerinin ilişkili şekilde birlikte değişkenlik göstermesi eğilimidir. Kovaryasyonu görmenin en iyi yolu iki veya daha fazla değişken arasındaki ilişkiyi görselleştirmektir. Bunu nasıl yapacağın yine ilişkili değişkenlerin türüne bağlıdır.
7.5.1 Bir kategorik ve bir sürekli değişken
Önceki sıklık poligonunda olduğu gibi kategorik bir değişkenle bölünen sürekli bir değişkenin dağılımını incelemeyi istemek yaygındır. Bu tür bir karşılatırma için geom_freqpoly() varsayılan görünümü o kadar faydalı değildir çünkü yükseklik sayı ile verilir. Yani, gruplardan biri diğerinden çok daha küçükse şekildeki farklılıkları görmek zordur. Örneğin, bir elmasın fiyatının kalitesine göre nasıl farklılık gösterdiğini araştıralım:
ggplot(data = diamonds, mapping = aes(x = price)) +
geom_freqpoly(mapping = aes(colour = cut), binwidth = 500)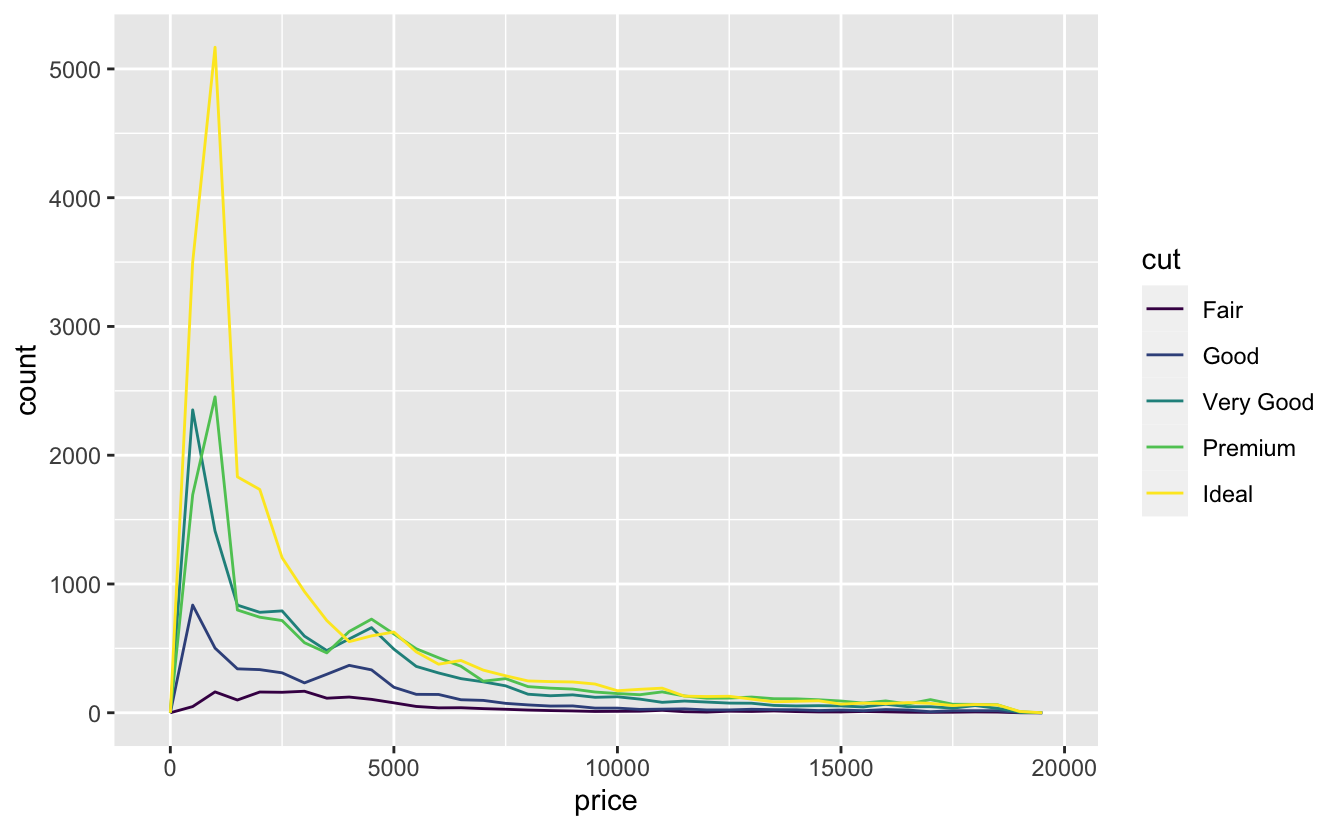
Dağılımdaki farklılığı görmek zordur çünkü toplam sayı çok farklılık gösterir:
ggplot(diamonds) +
geom_bar(mapping = aes(x = cut))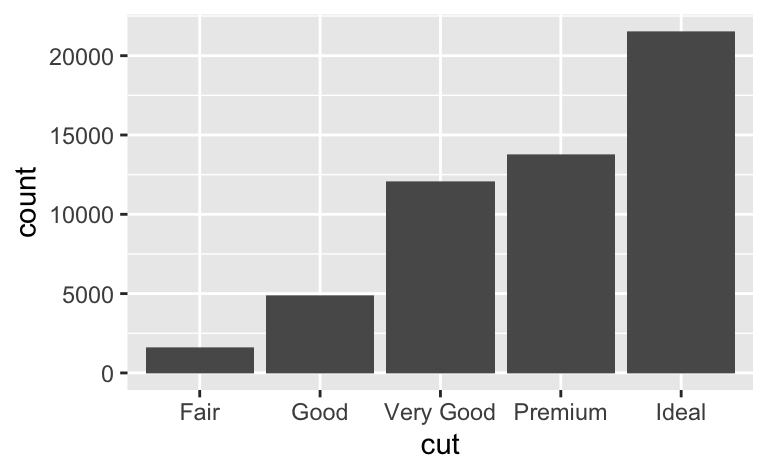
Karşılaştırmayı kolaylaştırmak için y ekseninde gösterileni değiştirmeliyiz. Sayımı göstermek yerine her sıklık poligonu altındaki alanın bir olduğu standartlaştırılmış yoğunluğu göstereceğiz.
ggplot(data = diamonds, mapping = aes(x = price, y = ..density..)) +
geom_freqpoly(mapping = aes(colour = cut), binwidth = 500)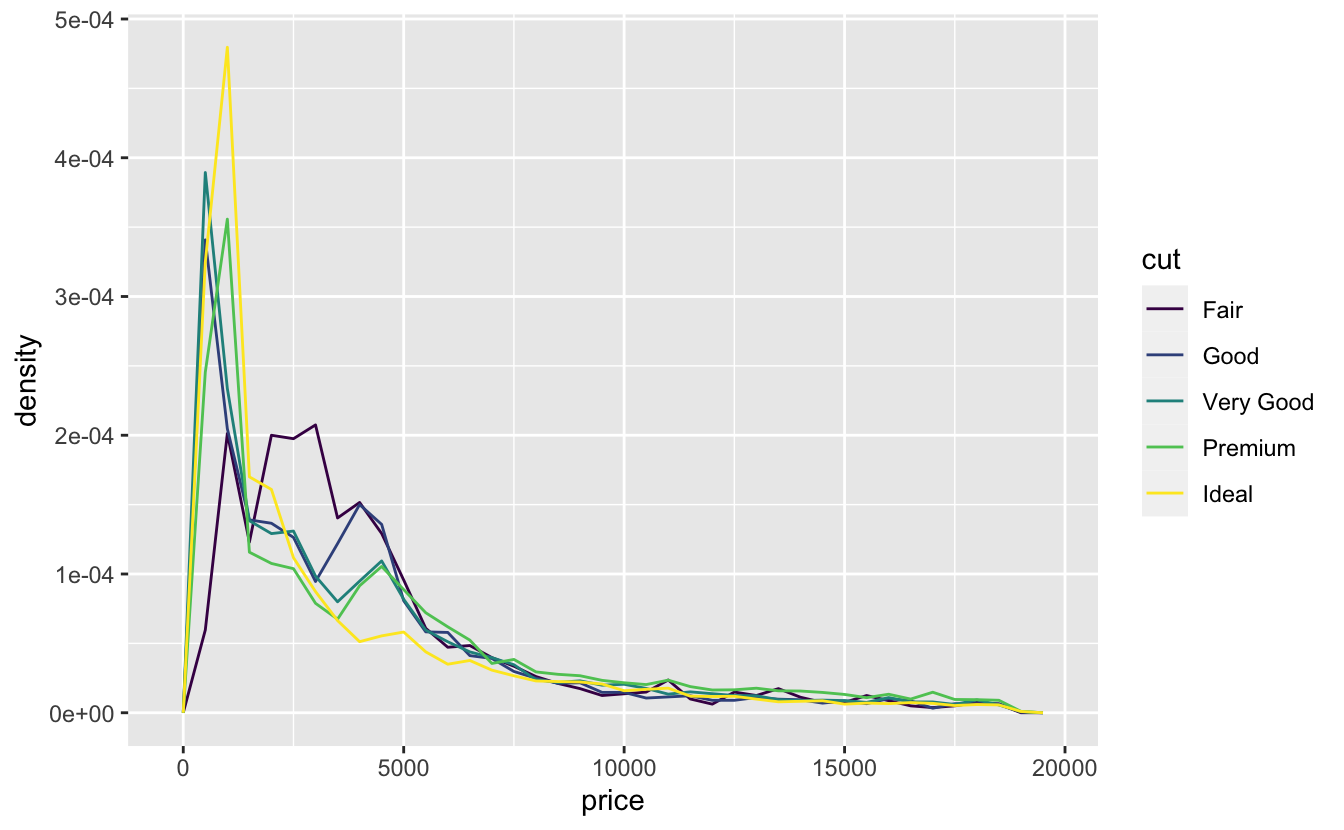
Bu grafikte şaşırtıcı bir şey var - vasat elmasların (en düşük kalite) en yüksek ortalama fiyata sahip olduğu görülüyor! Ama bunun nedeni belki de sıklık poligonlarının yorumlanmasının biraz zor olması olabilir - bu grafikte çok şey dönüyor.
Kategorik bir değişkenle bölünen sürekli bir değişkenin dağılımını göstermenin başka alternatif bir yolu kutu grafiğidir. Kutu grafiği istatistikçiler arasında popüler olan değer dağılımının görsel bir tür gösterimidir. Her kutu grafiği aşağıdakileri içerir:
Dağılımın, çeyrekler arası aralık (ÇAA) olarak bilinen bir mesafede 25 yüzdelik diliminden 75 yüzdelik dilimine uzanan bir kutu. Kutunun ortasında medyanı yani dağılımın 50 yüzdelik dilimini gösteren bir çizgi. Bu üç çizgi size dağılımın yayılışına ve dağılımın medyandan itibaren simetrik mi yoksa bir tarafa çarpık mı olduğuna dair bir bilgi verir.
Kutunun herhangi bir kenarından 1,5 kattan fazla ÇAA uzağa düşen gözlemleri gösteren görsel noktalar. Bu uç noktalar sıradışıdır bu nedenle ayrı grafiğe aktarılır.
Kutunun her iki ucundan uzanan ve dağılımdaki en uzak uç değer olmayan noktaya kadar giden bir çizgi (veya bıyık).
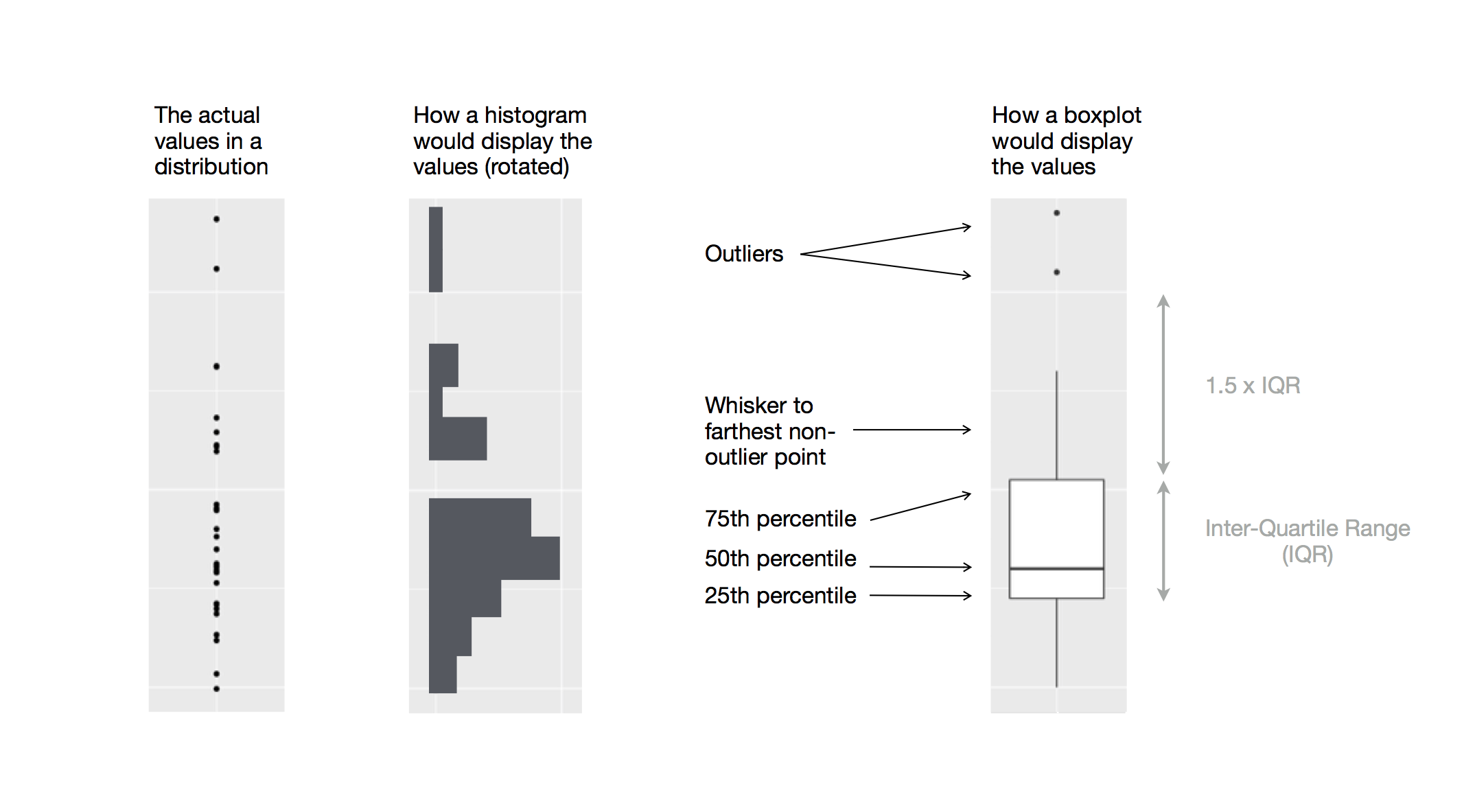
geom_boxplot() kullanarak kesime göre fiyat dağılımına bir bakalım:
ggplot(data = diamonds, mapping = aes(x = cut, y = price)) +
geom_boxplot()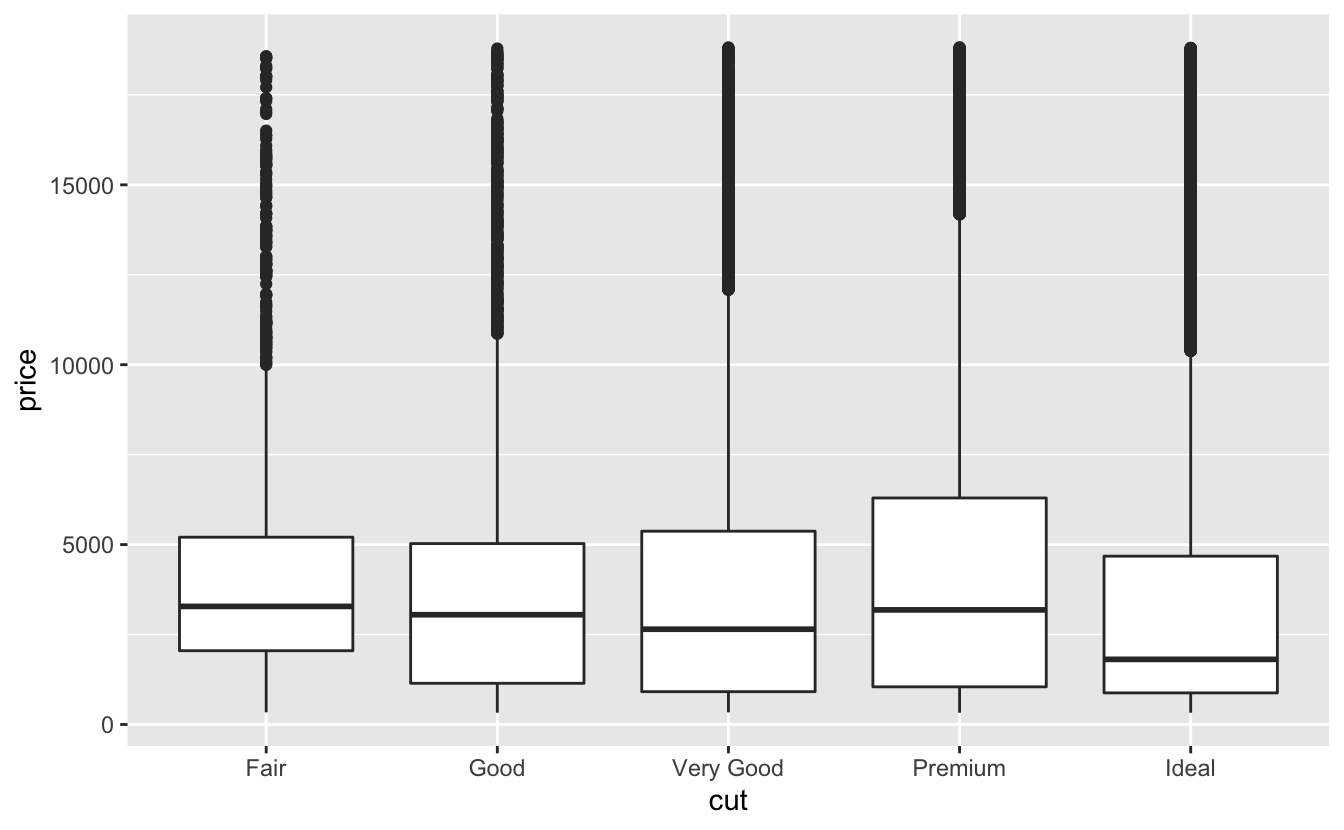
Dağılım hakkında çok daha az bilgi görüyoruz fakat kutu grafikler çok daha sıkıştırılmış bu nedenle bunları daha kolay karşılaştırabiliriz (ve bir grafiğe birden fazla sığdırabiliriz). Daha iyi kalitedeki elmasların ortalama daha ucuz olduğuna dair mantık dışı bulguyu destekler. Alıştırmalarda bunun nedenini bulmaya çalışacaksınız.
cut (kesme) sıralı bir faktördür: fena olmayan (fair), iyiden daha kötü, iyi çok iyiden daha kötü, vb. Çoğu kategorik değişken böyle yerleşik bir sıraya sahip değildir. Bu yüzden daha bilgi verici bir görüntü elde etmek için bunları yeniden sıralamanız gerekebilir. Bunu yapmanın bir yolu reorder() fonksiyonudur.
Örneğin, mpg veri setindeki class değişkenini alın. Otoban mesafelerinin sınıflara göre nasıl değiştiğini bilmek isteyebilirsiniz:
ggplot(data = mpg, mapping = aes(x = class, y = hwy)) +
geom_boxplot()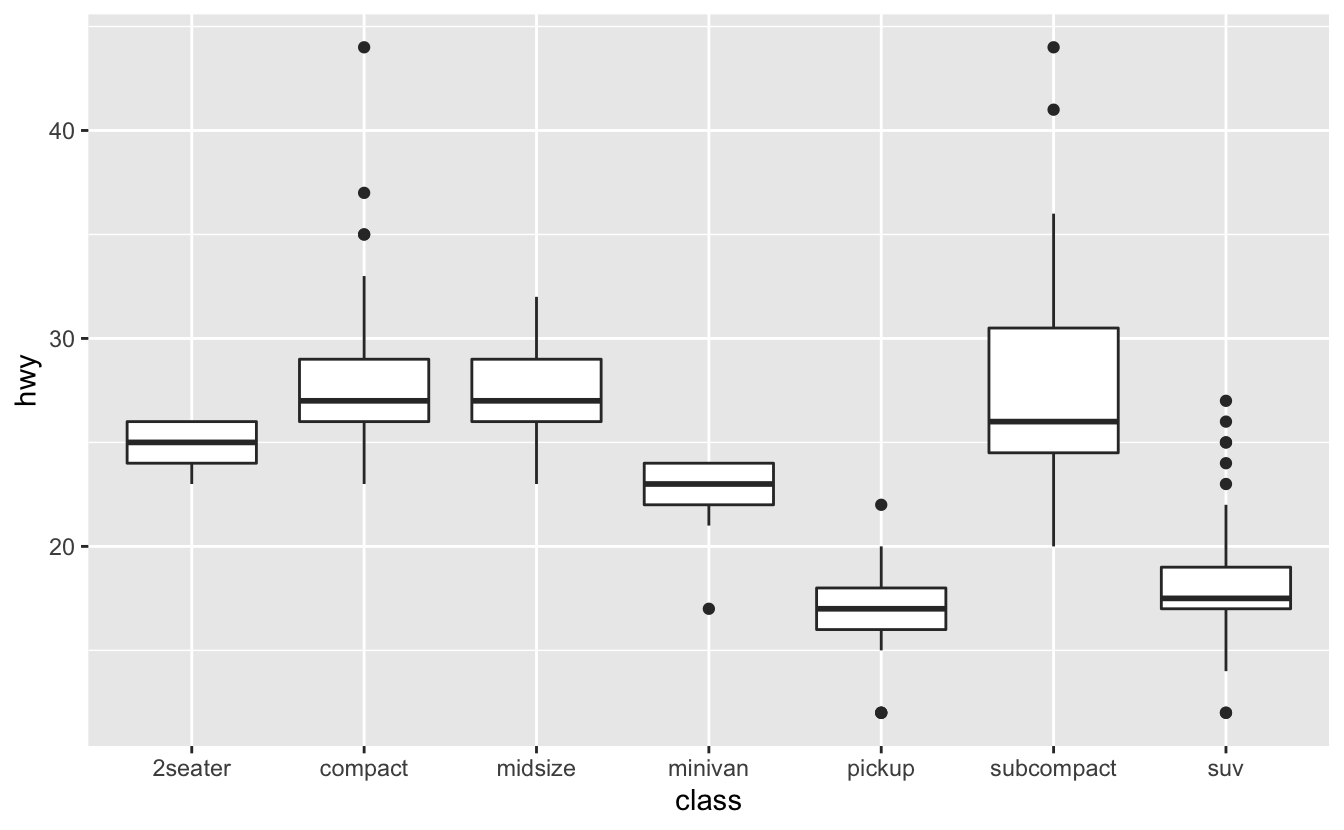
Eğilimin daha kolay görünmesini sağlamak için hwy medyan değeri temelinde classı yeniden sıralayabiliriz:
ggplot(data = mpg) +
geom_boxplot(mapping = aes(x = reorder(class, hwy, FUN = median), y = hwy))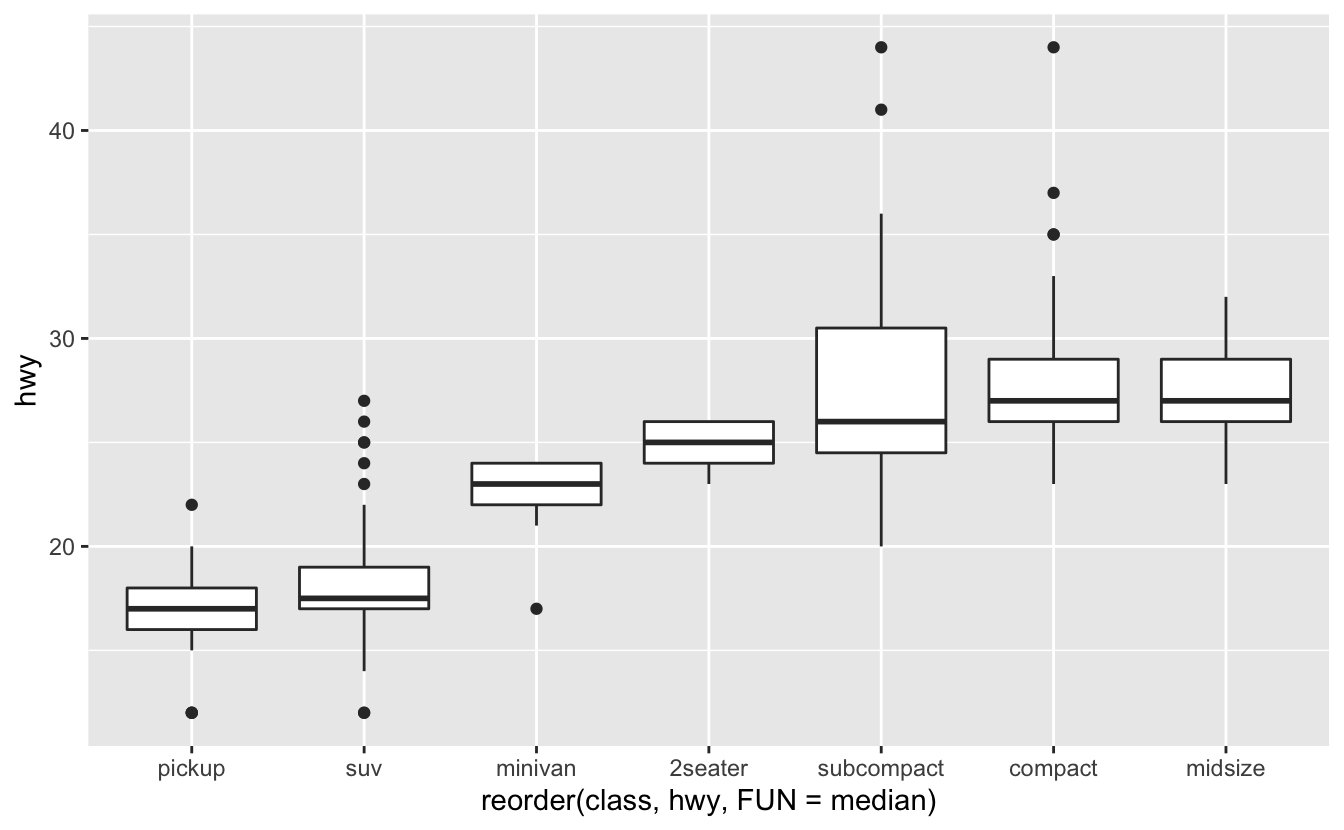
Değişken isimleriniz uzunsa, geom_boxplot()’ı 90 derece çevirirseniz daha iyi görünecektir. Bunu coord_flip() ile yapabilirsiniz.
ggplot(data = mpg) +
geom_boxplot(mapping = aes(x = reorder(class, hwy, FUN = median), y = hwy)) +
coord_flip()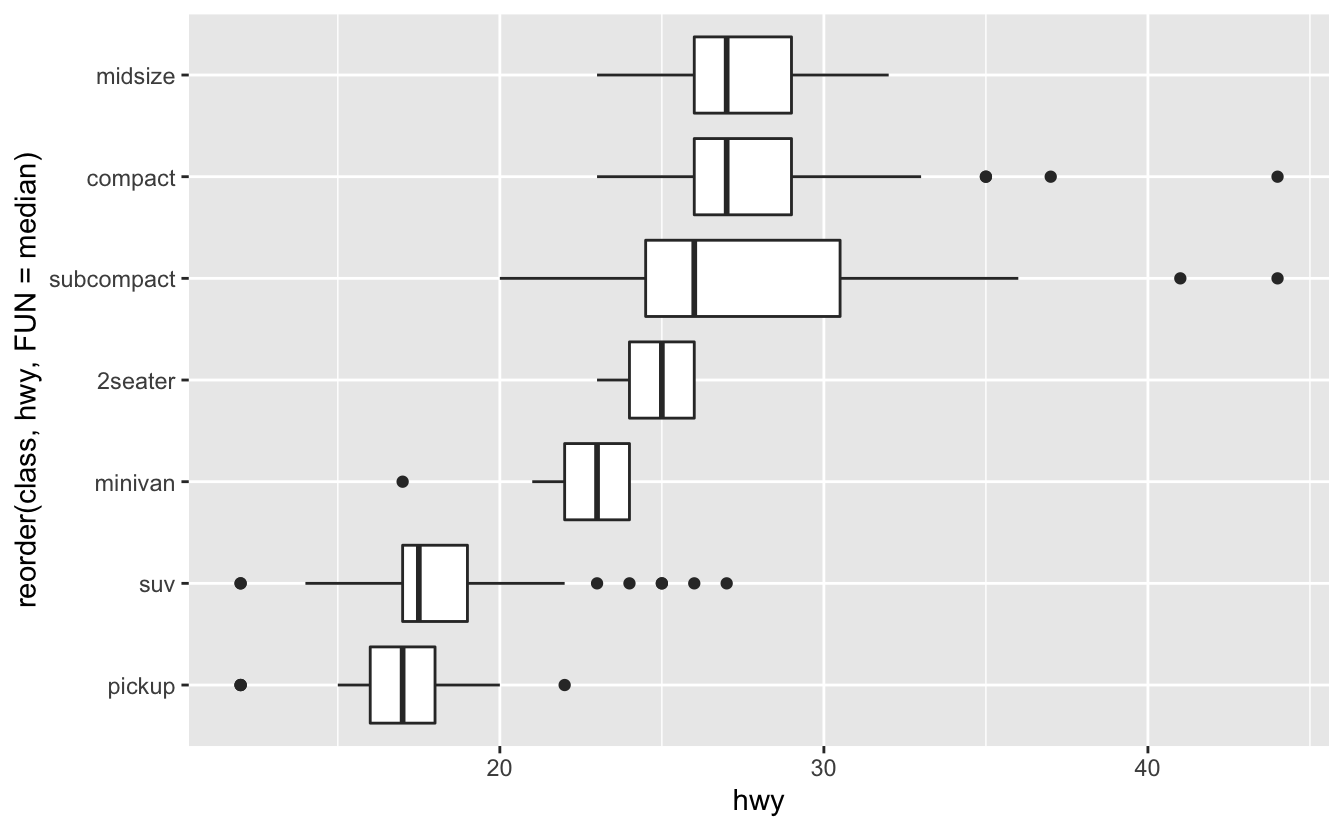
7.5.1.1 Alıştırmalar
İptal edilen ve iptal edilmeyen uçuşların kalkış zamanlarının görselleştirilmesini iyileştirmek için öğrendiklerinizi kullanın.
Bir elmasın fiyatını tahmin ederken elmas veri setinde en önemli değişken hangisidir? Bu değişken kesim ile nasıl korelasyon gösterir? Bu iki ilişkinin kombinasyonu neden daha düşük kaliteli elmasların daha pahalı olmasına yol açıyor?
ggstance paketini kurun ve yatay bir kutu grafiği oluşturun. Bu
coord_flip()kullanımı ile karşılaştırıldığında nasıldır?Kutu grafikleri kullanmadaki problem çok daha küçük veri setleri olan bir zamanda geliştirilmiş olmasından ve kabul edilemez sayıda “uç değerler” gösterme eğiliminde olmasından kaynaklanır. Bu problemi çözmek için bir yaklaşım harf değeri grafiğidir. lvplot paketini kurun ve fiyata karşı kesim dağılımını göstermek için
geom_lv()kullanmayı deneyin. Ne öğreniyorsunuz? Grafikleri nasıl yorumluyorsunuz?Dik kesilmiş
geom_histogram()veya renkligeom_freqpoly()ilegeom_violin()i karşılaştırın. Her iki yöntemin avantaj ve dezavantajları nelerdir?Küçük bir veri setiniz varsa sürekli ve kategorik değişkenler arasındaki ilişkiyi görmek için bazen
geom_jitter()kullanmak faydalıdır. ggbeeswarm paketigeom_jitter()ile benzer bazı yöntemler sağlar. Bunları sıralayın ve her birinin ne yaptığını kısaca açıklayın.
7.5.2 İki kategorik değişken
Kategorik değişkenler arasındaki kovaryasyonu görselleştirmek için her kombinasyon için gözlem sayısını hesaplamalısınız Bunu yapmanın bir yolu yerleşik geom_count() fonksiyonunu kullanmaktır:
ggplot(data = diamonds) +
geom_count(mapping = aes(x = cut, y = color))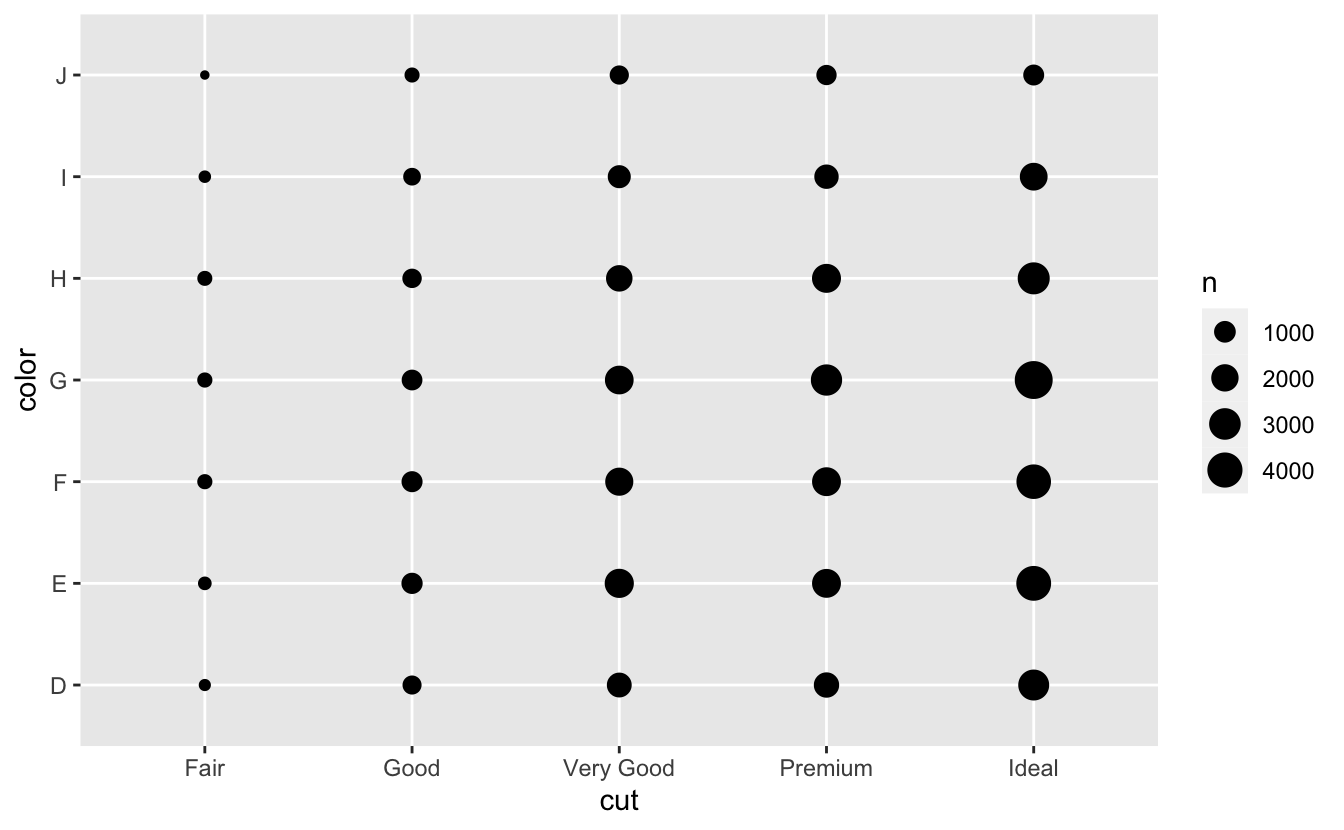
Grafikteki her dairenin boyutu her değer kombinasyonunda kaç gözlem olduğunu gösterir. Kovaryasyon belirli x değerleri ve belirli y değerleri arasında güçlü korelasyon olarak görünecektir.
Başka bir yaklaşım ise dplyr ile sayıyı hesaplamaktır:
diamonds %>%
count(color, cut)
#> # A tibble: 35 × 3
#> color cut n
#> <ord> <ord> <int>
#> 1 D Fair 163
#> 2 D Good 662
#> 3 D Very Good 1513
#> 4 D Premium 1603
#> 5 D Ideal 2834
#> 6 E Fair 224
#> # … with 29 more rowsArdından geom_tile() ve dolgu estetiği ile görselleştirin:
diamonds %>%
count(color, cut) %>%
ggplot(mapping = aes(x = color, y = cut)) +
geom_tile(mapping = aes(fill = n))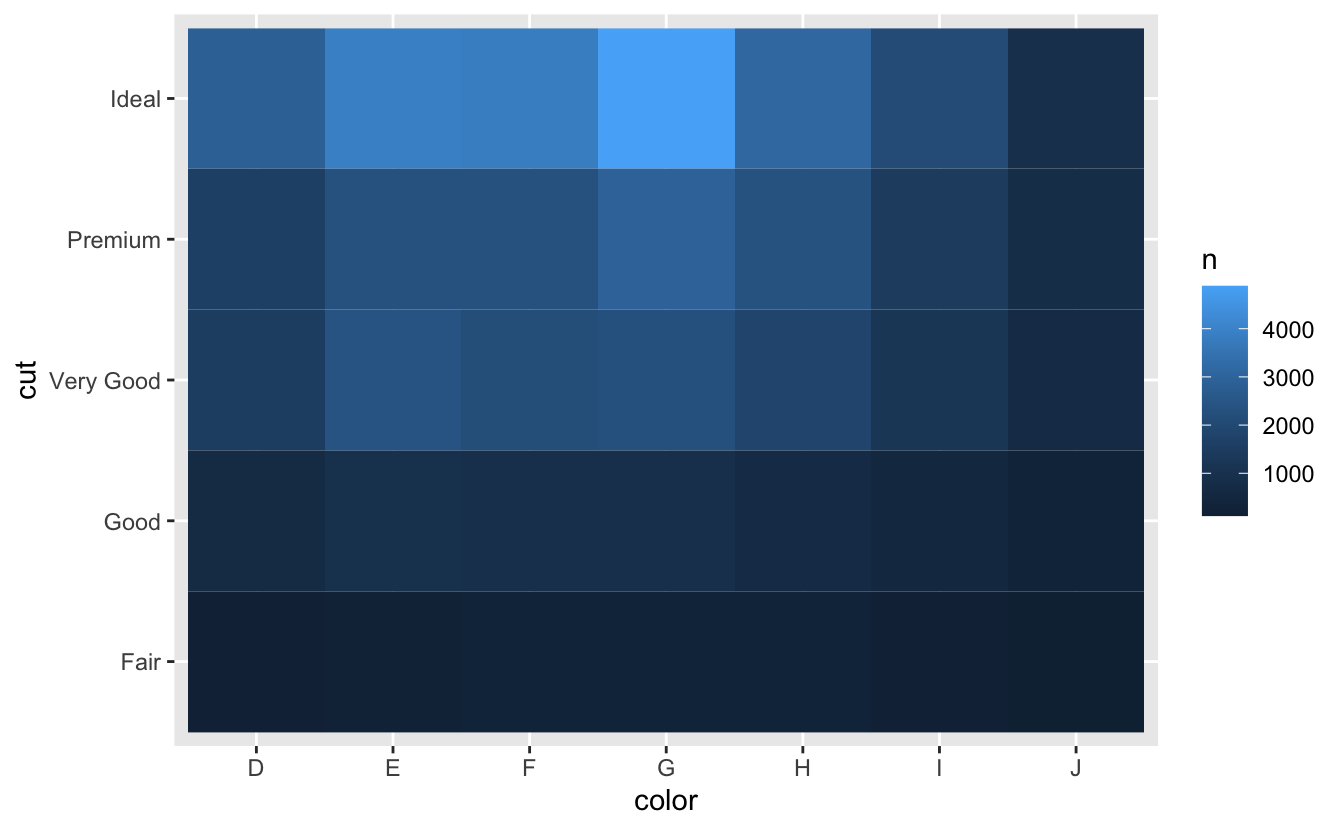
Kategorik değişkenler sıralı değilse ilginç örüntüleri daha açık bir şekilde ortaya çıkarmak için sütun ve sıraları aynı anda yeniden düzenlemek için seriation paketini kullanabilirsiniz. Daha geniş grafikler için interaktif grafikler oluşturan d3heatmap veya heatmaply paketlerini denemek isteyebilirsiniz.
7.5.2.1 Alıştırmalar
Renk içinde kesim veya kesim içinde renk dağılımını daha açıkça göstermek için yukarıdaki sayım veri setini nasıl tekrar ölçeklendirebilirsiniz?
Ortalama uçuş gecikmelerinin varış yeri ve aya göre nasıl değiştiğini araştırmak için dplyr ile birlikte
geom_tile()kullanın. Grafiğin okunmasını zorlaştıran ne? Bunu nasıl düzeltebilirsiniz?Yukarıdaki örnekte
aes(x = color, y = cut)kullanmak nedenaes(x = cut, y = color)kullanmaktan biraz daha iyi?
7.5.3 İki sürekli değişken
İki sürekli değişken arasındaki kovaryasyonu görselleştirmenin harika bir yolunu zaten gördünüz: geom_point() ile bir dağılım grafiği çizin. Noktalardan oluşan örüntüde kovaryasyonu görebilirsiniz. Örneğin, karat boyutu ve elmas fiyatı arasındaki üssel ilişkiyi görebilirsiniz.
ggplot(data = diamonds) +
geom_point(mapping = aes(x = carat, y = price))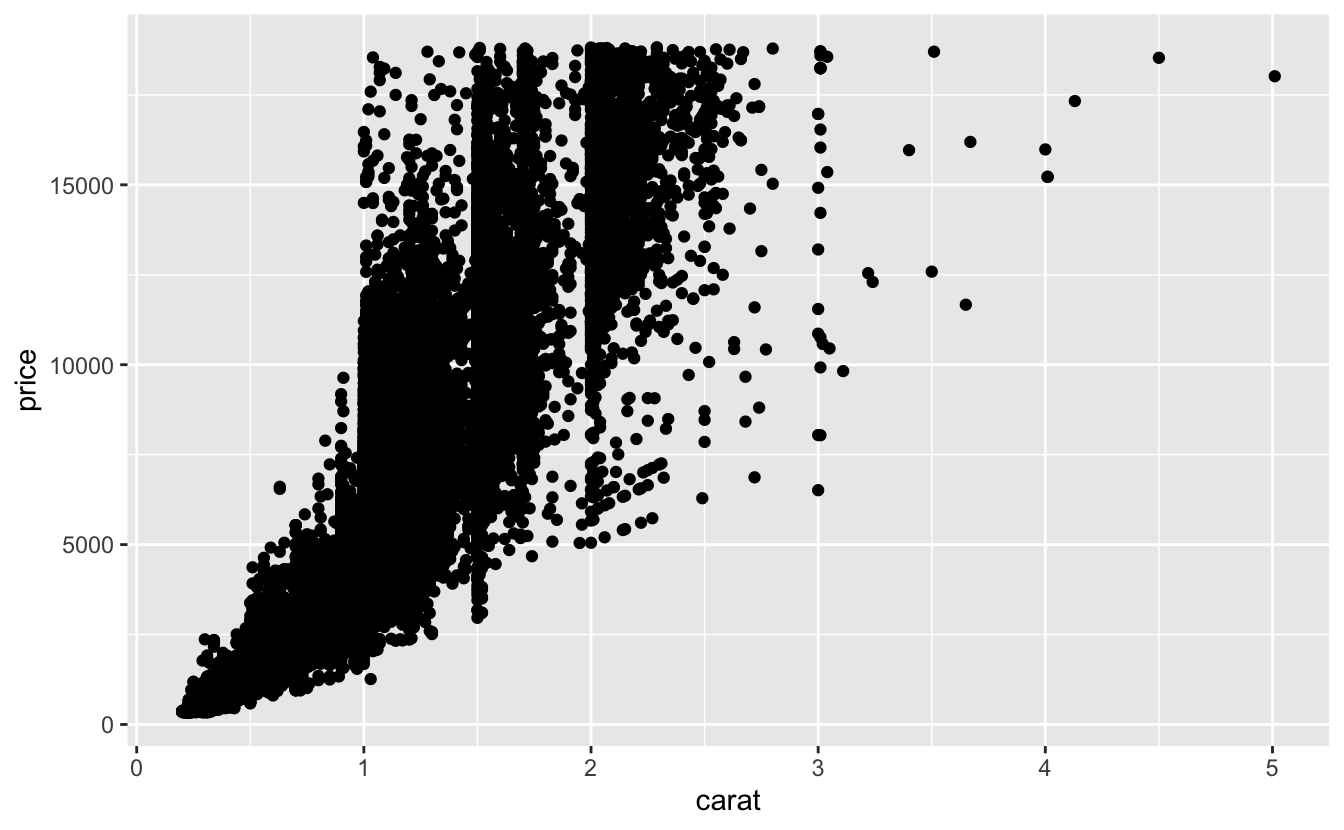
Veri setinizin boyutu arttıkça dağılım grafikleri daha az faydalı hale gelir çünkü noktalar üst üste gelmeye başlar ve birikerek sadece siyah alanlar oluşturur (yukarıdaki gibi).
Problemi çözmenin bir yolunu zaten gördün: şeffalık eklemek için alpha estetiği kullanmak.
ggplot(data = diamonds) +
geom_point(mapping = aes(x = carat, y = price), alpha = 1 / 100)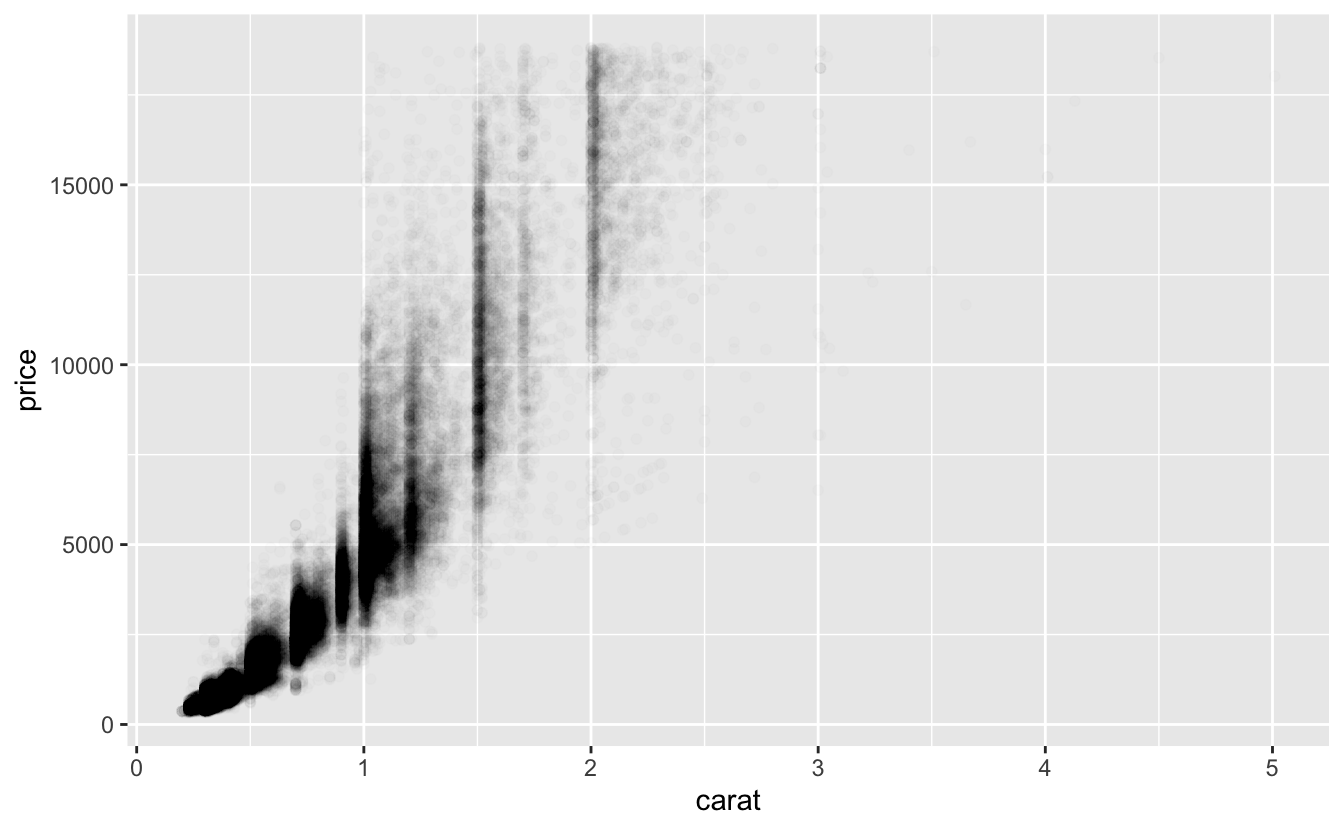
Fakat şeffaflık kullanmak çok geniş veri setleri için zorlayıcı olabilir. Başka bir çözüm kutu kullanmaktır. Daha önce bir boyutta kutulamak için geom_histogram() ve geom_freqpoly() kullandınız. Şimdi iki boyutta kutulamak için geom_bin2d() ve geom_hex()i nasıl kullanacağınızı öğreneceksiniz.
geom_bin2d() ve geom_hex() koordinat düzlemini 2 boyutlu kutulara böler ve her kutuya kaç nokta düştüğünü göstermek için bir dolgu rengi kullanır.geom_bin2d() dikdörtgen kutular oluşturur. geom_hex() altıgen kutular oluşturur. geom_hex() kullanmak için hexbin paketini kurmanız gerekecek.
ggplot(data = smaller) +
geom_bin2d(mapping = aes(x = carat, y = price))
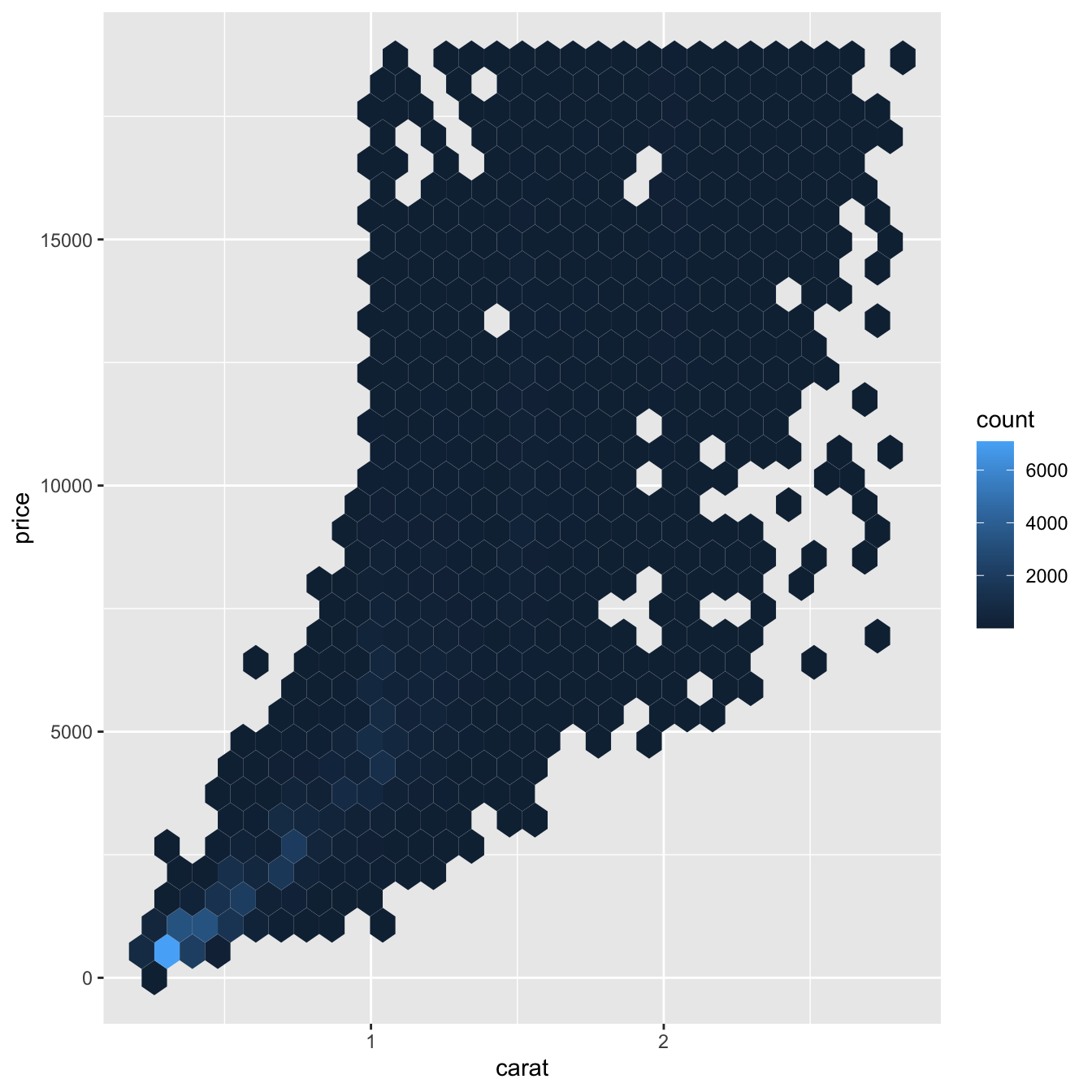
# install.packages("hexbin")
ggplot(data = smaller) +
geom_hex(mapping = aes(x = carat, y = price))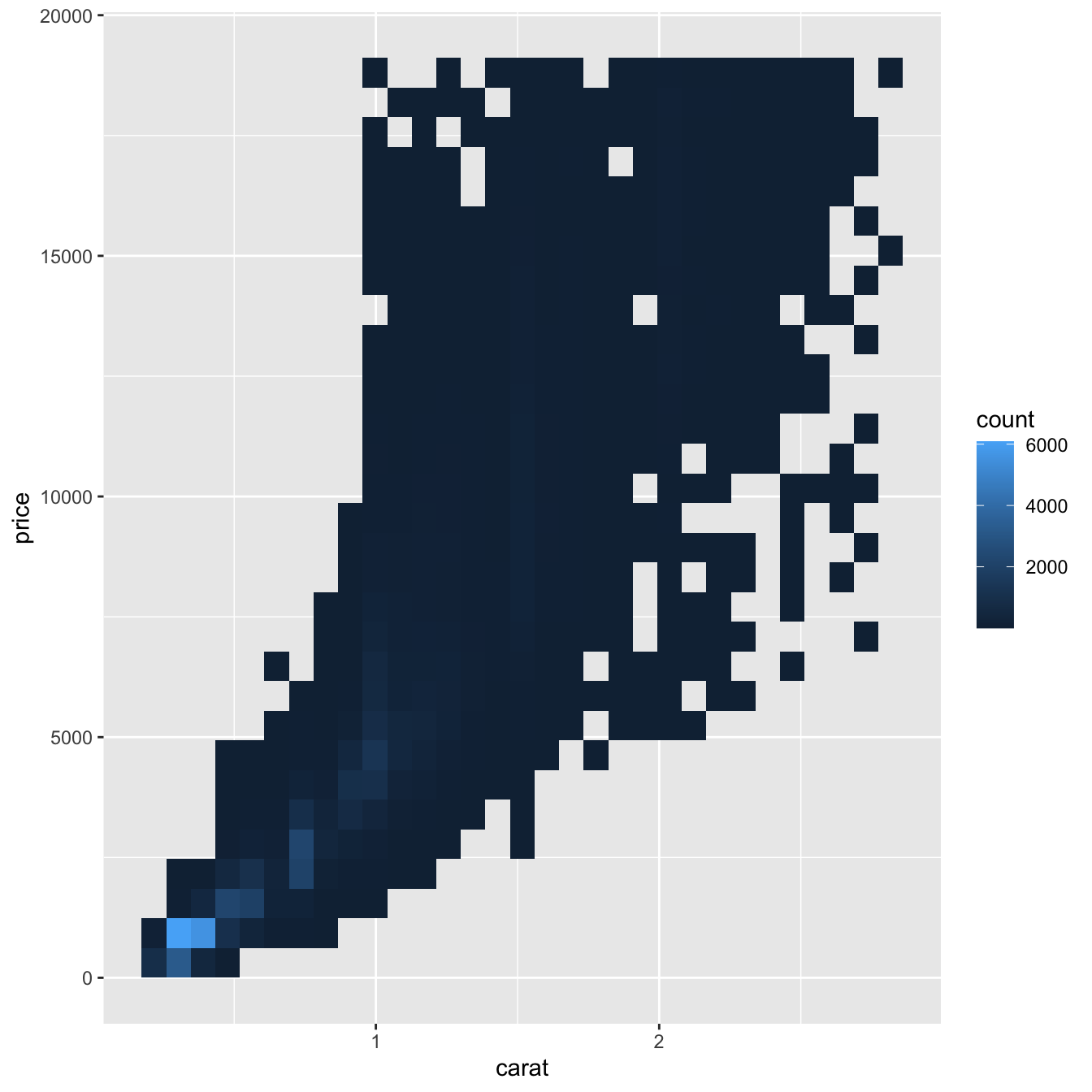
Başka bir seçenek bir sürekli değişkeni gruplamaktır. Böylece kategorik bir değişken gibi davranır. Daha sonra öğrendiğiniz bir kategorik ve sürekli değişken kombinasyonunu görselleştirme tekniklerinden birini kullanabilirsiniz. Örneğin caratı gruplayabilirsiniz ve sonra her grup için bir kutu grafiği oluşturabilirsiniz:
ggplot(data = smaller, mapping = aes(x = carat, y = price)) +
geom_boxplot(mapping = aes(group = cut_width(carat, 0.1)))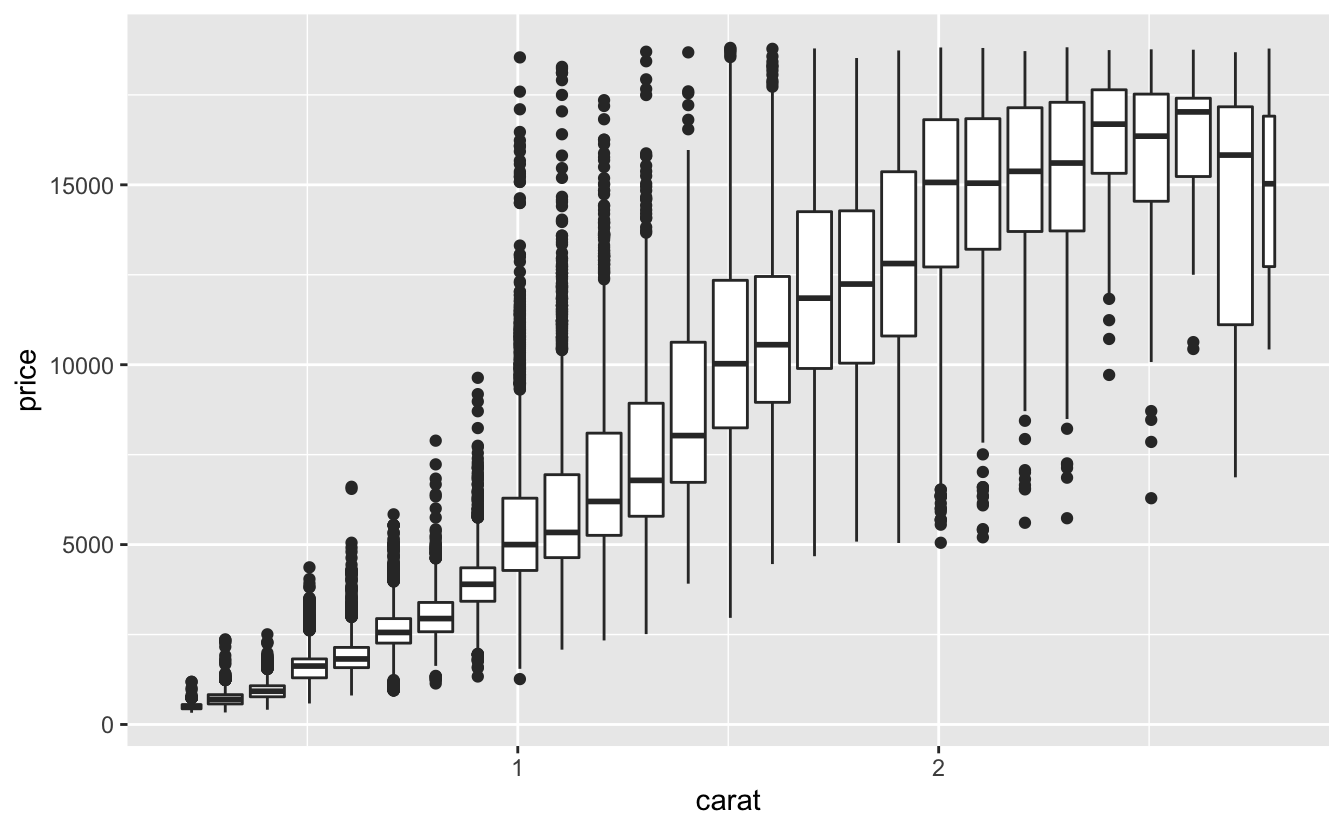
Yukarıda kullanıldığı gibi cut_width(x, width), xi genişlik width kutularına böler. Varsayılan durumda kutu grafikleri ne kadar gözlem olduğundan bağımsız olarak kabaca aynı görünür (uç değerlerin sayısı dışında), bu yüzden her kutu grafiğinin farklı sayıda noktayı özetlediğini söylemek zordur. Bunu göstermenin bir yolu varwidth = TRUE ile kutu grafiğinin genişliğini nokta sayısı ile oratılı yapmaktır.
Başka bir yaklaşım her kutudaki nokta sayısını yaklaşık olarak aynı göstermektir. Bu, cut_number() ile yapılır:
ggplot(data = smaller, mapping = aes(x = carat, y = price)) +
geom_boxplot(mapping = aes(group = cut_number(carat, 20)))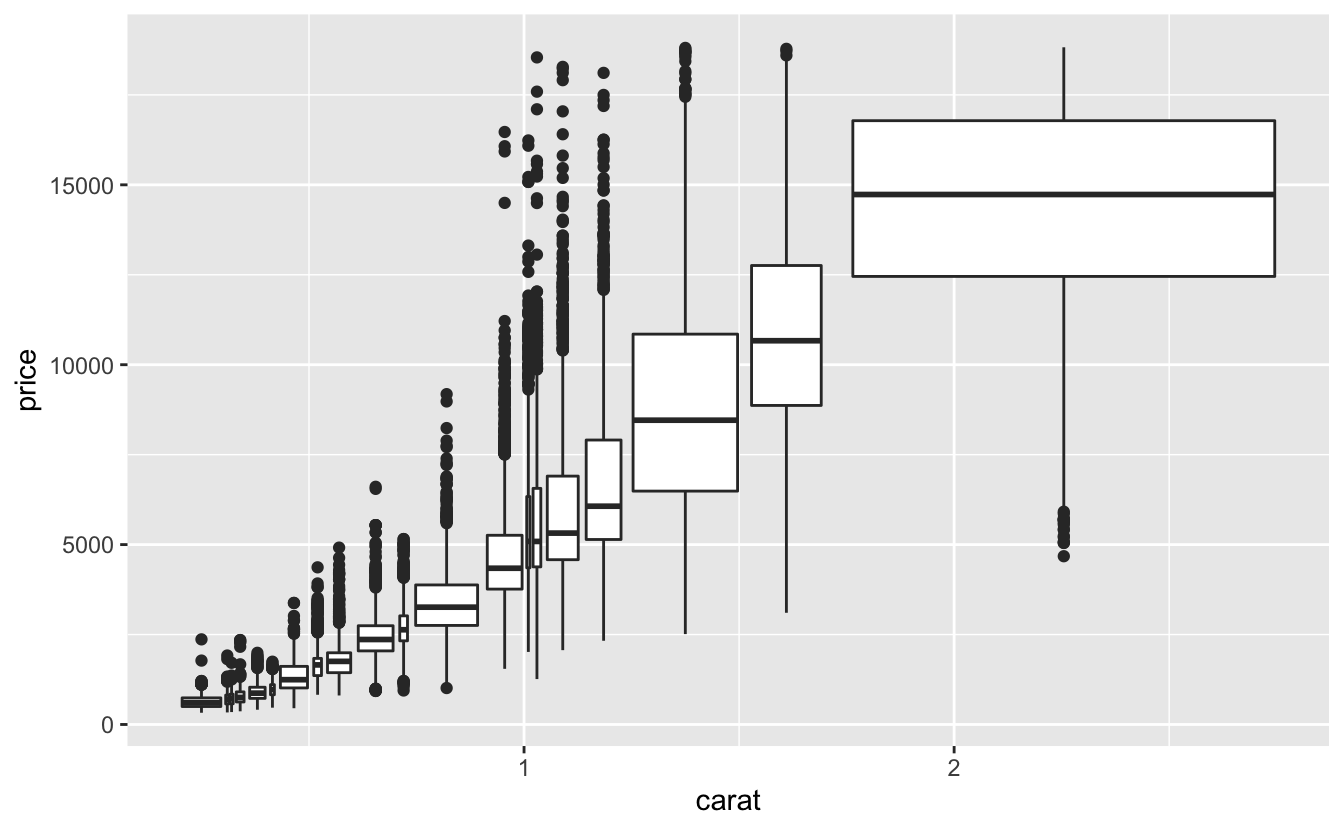
7.5.3.1 Alıştırmalar
Koşullu dağılımı kutu grafiğiyle özetlemek yerine frekans poligonu kullanabilirsiniz.
cut_width()veyacut_number()kullanırken neyi göz önünde bulundurmalısınız? Bu,caratveprice2 boyutlu dağılımının görselleştirilmesini nasıl etkiler?Fiyata göre bölünmüş olarak karat dağılımını görselleştirin.
Çok büyük elmasların fiyat dağılımı küçük elmaslara kıyasla nasıldır? Beklediğiniz gibi mi yoksa sizi şaşırtıyor mu?
Kesim, karat ve fiyatın birlikte dağılımını görselleştirmek için öğrendiğiniz tekniklerin ikisini birleştirin.
İki boyutlu grafikler tek boyutlu grafiklerde görünmeyen uç değerleri görünür hale getirir. Örneğin, aşağıdaki grafikteki bazı noktalar
xveydeğerlerinin sıradışı bir kombinasyonuna sahiptir. Bu kombinasyonxveydeğerleri ayrı ayrı incelendiğinde normal göründüğü halde noktaları uç değer yapar.ggplot(data = diamonds) + geom_point(mapping = aes(x = x, y = y)) + coord_cartesian(xlim = c(4, 11), ylim = c(4, 11))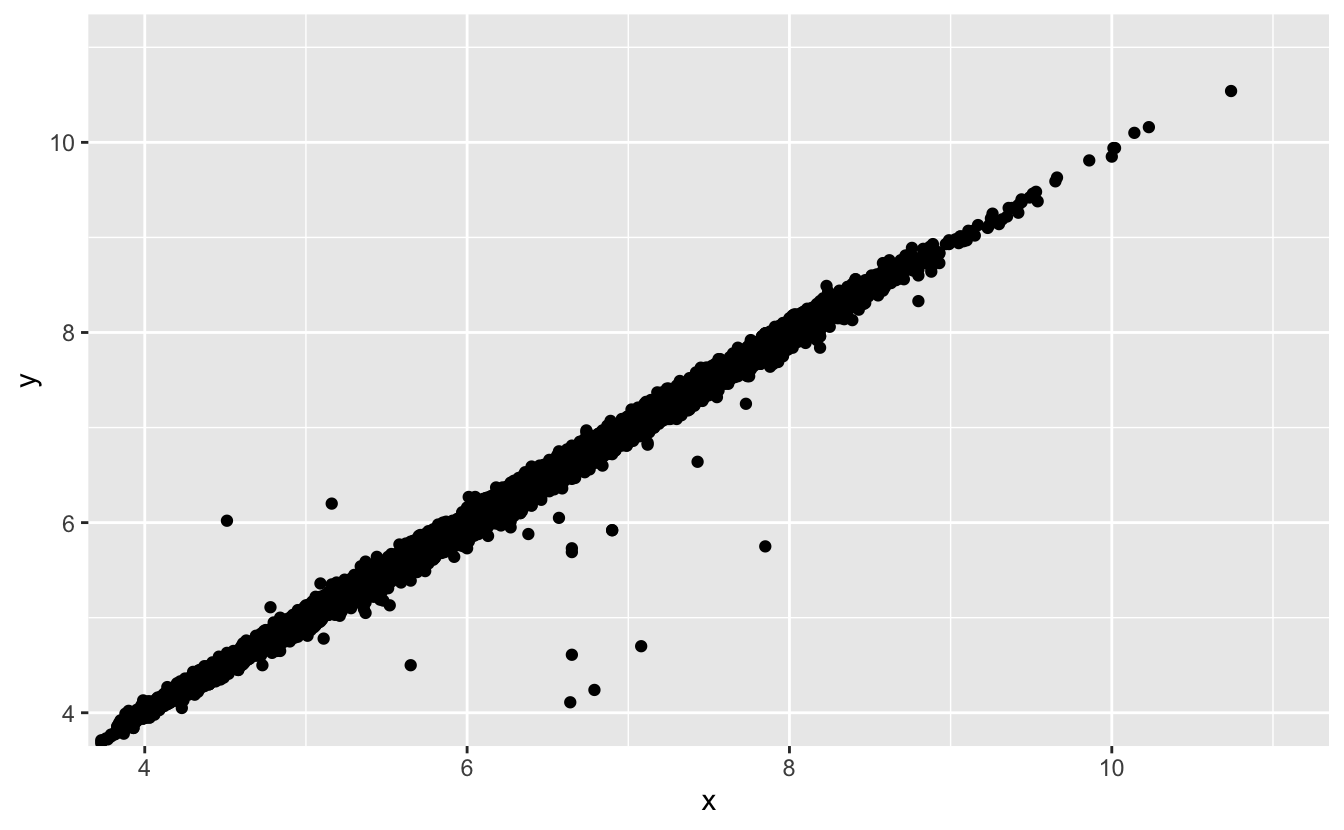
Neden dağılım grafiği bu durumda gruplu grafikten daha iyi bir görüntüye sahip?
7.6 Örüntüler ve modeller
Verilerinizdeki örüntüler ilişkiler hakkında ipuçları sağlar. İki değişken arasında sistematik bir ilişki varsa veride bir örüntü olarak görünecektir. Bir örüntü farkederseniz kendinize şunları sorun:
Bu örüntü tesadüf eseri olabilir mi (yani, rasgele)?
Örüntünün dolaylı olarak gösterdiği ilişkiyi nasıl tanımlayabilirsiniz?
Örüntünün dolaylı olarak gösterdiği ilişki ne kadar güçlü?
İlişkiyi başka hangi değişkenler etkileyebilir?
Ayrı ayrı veri alt gruplarına bakarsan ilişki değişir mi?
Old Faithful püskürme uzunluklarının püskürmeler arasındaki bekleme süresine karşı dağılım grafiği bir örüntü gösterir: daha uzun bekleme süreleri daha uzun püskürmelerle ilişkili. Dağılım grafiği aynı zamanda yukarıda farkettiğimiz iki kümeyi gösterir.
ggplot(data = faithful) +
geom_point(mapping = aes(x = eruptions, y = waiting))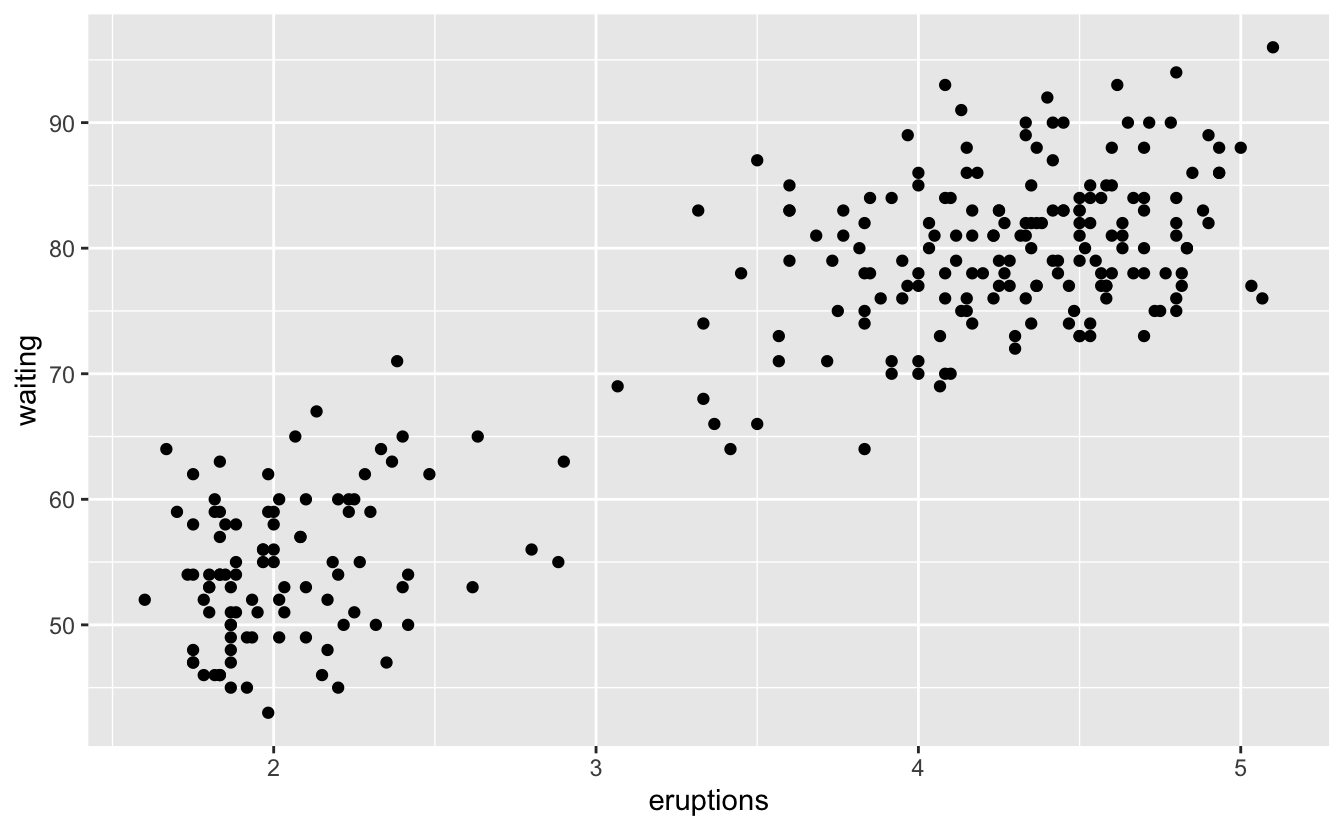
Örüntüler veri bilimciler için en kullanışlı araçlardan birini sağlar çünkü kovaryasyonu gösterirler. Varyasyonun belirsizlik oluşturan bir fenomen olduğunu düşünürseniz kovaryasyon bunu azaltn bir fenomendir. İki değişken birlikte değişkenlik gösterirse, bir değişkenin değerlerini ikincisi hakkında daha iyi tahminler yapmada kullanabilirsiniz. Kovaryasyon nedensel ilişkiye bağlıysa (özel bir durum), bir değişkenin değerini ikinci değişkenin değerini kontrol etmek için kullanabilirsiniz.
Modeller verilerden örüntüler elde edilmesinde bir araçtır. Örneğin elmas verisini düşünün. Kesim ve fiyat arasındaki ilişkiyi anlamak zordur çünkü kesim ve karat ve karat ve fiyat sıkı ilişki içindedir. Fiyat ve karat arasındaki çok güçlü ilişkiyi ortadan kaldırmak için bir model kullanmak mümkündür. Bu şekilde geri kalan incelikleri araştırabiliriz. Aşağıdaki kod carattan priceı tahmin eden ve ardından artık değerleri (tahmin edilen ve gerçek değer arasındaki fark) hesaplayan bir model oluşturur. Artık değerler bize karatın etkisi çıkarıldıktan sonra elmasın fiyatına bir bakış verir.
library(modelr)
mod <- lm(log(price) ~ log(carat), data = diamonds)
diamonds2 <- diamonds %>%
add_residuals(mod) %>%
mutate(resid = exp(resid))
ggplot(data = diamonds2) +
geom_point(mapping = aes(x = carat, y = resid))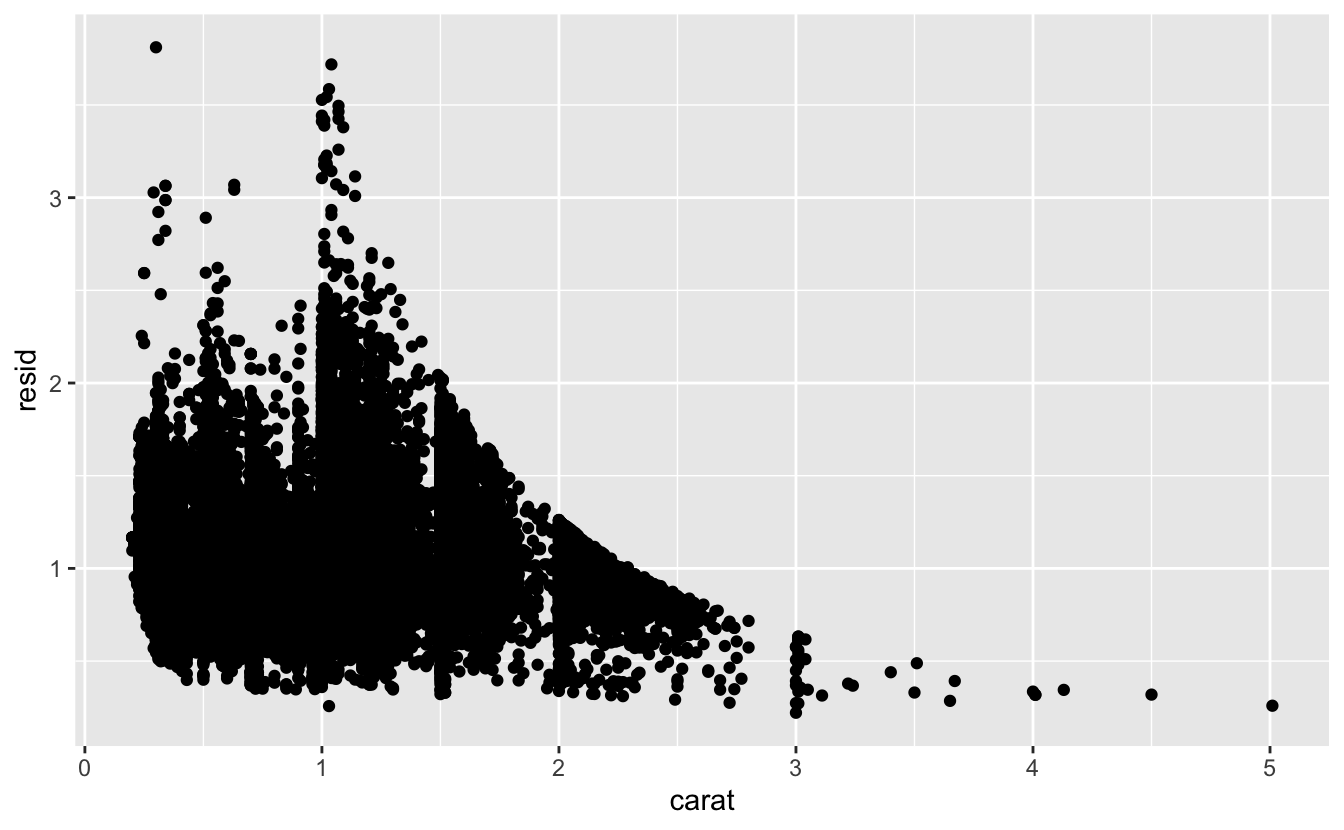
Karat ve fiyat arasındaki güçlü ilişkiyi çıkardıktan sonra kesim ve fiyat arasındaki ilişkide neyi bekleyebileceğinizi görebilirsiniz: boyutlarına göre daha iyi kaliteli elmaslar daha pahalıdır.
ggplot(data = diamonds2) +
geom_boxplot(mapping = aes(x = cut, y = resid))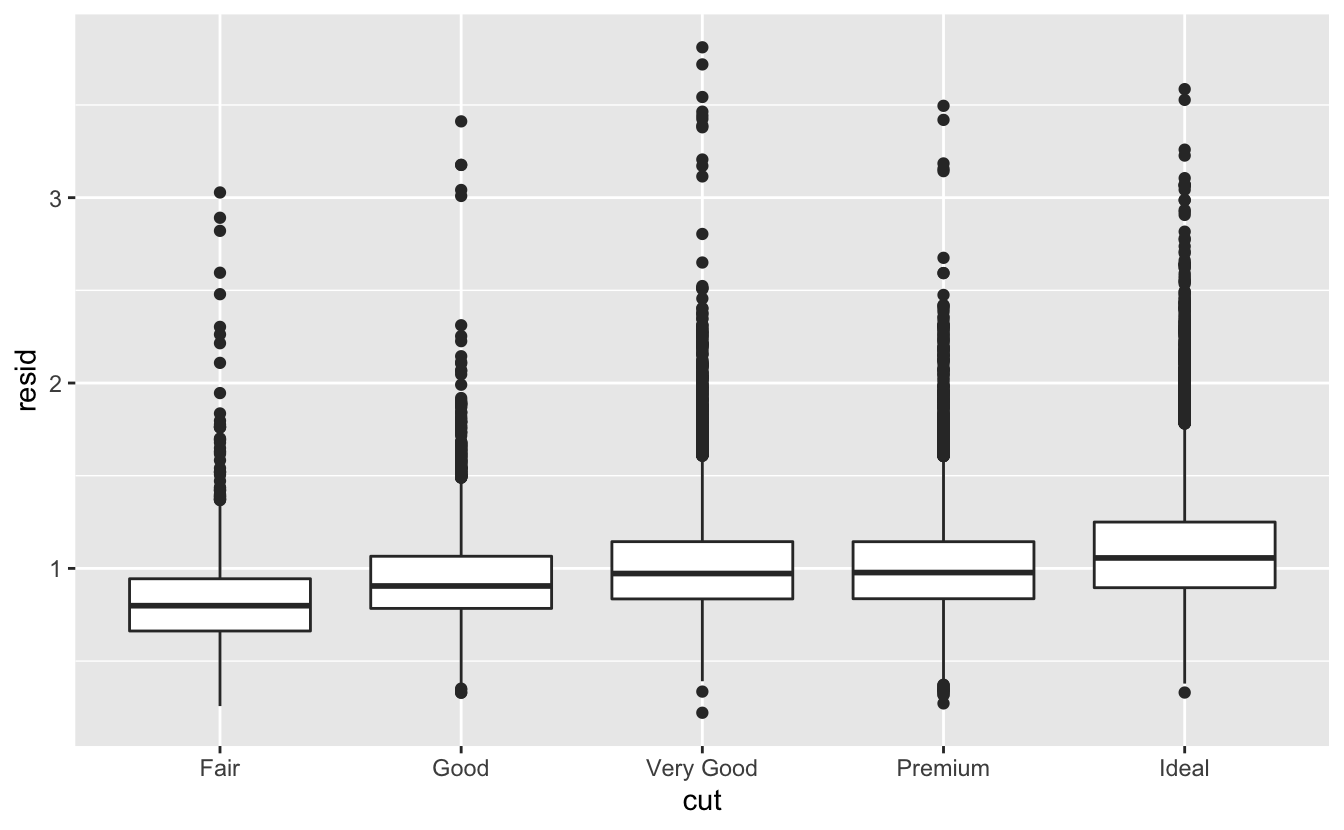
Modeller ve modelr paketinin nasıl çalıştığını kitabın son kısmında öğreneceksiniz model. Modellemeyi daha sonraya bırakıyoruz çünkü veri düzenleme ve programlama araçlarınız olduktan sonra modellerin ne olduğunu ve nasıl çalıştığını anlamak daha kolay.
7.7 ggplot2 çağrıları
Bu giriş bölümlerinden sonra ggplot2 kodunun daha kısa bir ifadesine geçiş yapacağız. Şu ana kadar öğrenirken neyin faydalı olduğuna dair çok açıktık:
ggplot(data = faithful, mapping = aes(x = eruptions)) +
geom_freqpoly(binwidth = 0.25)Tipik olarak, bir fonksiyona ilk veya ilk iki argüman o kadar önemlidir ki, ezbere bilmelisiniz. ggplot()a ilk iki argüman data ve mappingdir ve aes()e ilk iki argüman x ve ydir. Kitabın geri kalanında bu isimleri kullanmayacağız. Bu daha az yazmayı sağlar ve standart metin miktarını azaltarak grafikler arasında nelerin farklı olduğunu görmeyi kolaylaştırır. Bu, fonksiyonlar kısmında geri döneceğimiz çok önemli bir programalama bilgisidir.
Önceki grafikleri daha kısa yazarsak şöyle olur:
ggplot(faithful, aes(eruptions)) +
geom_freqpoly(binwidth = 0.25)Bazen bir veri dönüşümü akışının sonunu grafiğe çevireceğiz. %>%dan +a geçişe dikkat edin. Keşke bu geçiş gerekli olmasaydı ama ne yazık ki ggplot2 akış keşfedilmeden geliştirilmişti.
diamonds %>%
count(cut, clarity) %>%
ggplot(aes(clarity, cut, fill = n)) +
geom_tile()7.8 Daha fazla bilgi
ggplot2 mekanikleri hakkında daha fazla bilgi için ggplot2 kitabını edinmenizi şiddetle tavsiye ederim: https://amzn.com/331924275X. Yakın zamanda güncellendi ve bu yüzden dplyr ve tidyr kodunu içeriyor ve görselleştirmenin tüm yönlerini keşfetmek için daha fazla alana sahip. Ne yazık ki bu kitap genellikle ücretsiz edinilemiyor ancak bir üniversiteye bağlıysanız muhtemelen SpringerLink aracılığyla elektronik bir versiyonunu edinebilirsiniz.
Başka bir faydalı kaynak Winston Chang’ın R Graphics Cookbook. İçeriğin büyük bir kısmı http://www.cookbook-r.com/Graphs/ adresinde bulunabilir.
Aynı zamand Antony Unwin’in Graphical Data Analysis with R tavsiye ediyorum. Bu bölümde kapsanan materyale benzer bir kitap fakat çok daha derine iniyor.